Experimental Method

We performed empirical tests comparing the AIS-BN algorithm to the likelihood weighting (LW) and the self-importance sampling (SIS) algorithms. The two algorithms are basically the state of the art general purpose belief updating algorithms. The AA [Dagum et al.1995] and the bounded variance [Dagum and Luby1997] algorithms, which were suggested by a reviewer, are essentially enhanced special purpose versions of the basic LW algorithm. Our implementation of the three algorithms relied on essentially the same code with separate functions only when the algorithms differed. It is fair to assume, therefore, that the observed differences are purely due to the theoretical differences among the algorithms and not due to the efficiency of implementation. In order to make the comparison of the AIS-BN algorithm to LW and SIS fair, we used the first method of computation (Section 3.5), i.e., one that relies on single sampling rather than calling the basic AIS-BN algorithm twice.

We measured the accuracy of approximation achieved by the simulation in terms of the Mean Square Error (MSE), i.e., square root of the sum of square differences between Pr^$\prime$(x_ij) and Pr(x_ij), the sampled and the exact marginal probabilities of state j ( j = 1, 2,..., n_i) of node i, such that X_i$\notin$$\bf E$. More precisely,

MSE = $$\sqrt{\frac{1}{\sum_{X_{i}\in {\bf N}\backslash {\bf E}}n_{i}} \s... ...m_{j=1}^{n_{i}}({\mbox{\rm Pr}}^{\prime }(x_{ij})-{\mbox{\rm Pr}}(x_{ij}))^{2}}$$    ,

where $\bf N$ is the set of all nodes, $\bf E$ is the set of evidence nodes, and n_i is the number of outcomes of node i. In all diagrams, the reported MSE is averaged over 10 runs. We used the clustering algorithm [Lauritzen and Spiegelhalter1988] to compute the gold standard results for our comparisons of the mean square error. We performed all experiments on a Pentium II, 333 MHz Windows computer.

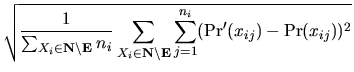While MSE is not perfect, it is the simplest way of capturing error that lends itself to further theoretical analysis. For example, it is possible to derive analytically the idealized convergence rate in terms of MSE, which, in turn, can be used to judge the quality of the algorithm. MSE has been used in virtually all previous tests of sampling algorithms, which allows interested readers to tie the current results to the past studies. A reviewer offered an interesting suggestion of using cross-entropy or some other technique that weights small changes near zero much more strongly than the equivalent size change in the middle of the [0, 1] interval. Such measure would penalize the algorithm for imprecisions of possibly several orders of magnitude in very small probabilities. While this idea is interesting, we are not aware of any theoretical reasons as to why this measure would make a difference in comparisons between AIS-BN, LW and SIS algorithms. The MSE, as we mentioned above, will allow us to compare the empirically determined convergence rate to the theoretically derived ideal convergence rate. Theoretically, the MSE is inversely proportional to the square root of the sample size.

Since there are several tunable parameters used in the AIS-BN algorithm, we list the values of the parameters used in our test: l = 2, 500; w^k = 0 for k $\leq$ 9 and w^k = 1 otherwise. We stopped the updating process in Step 7 of Figure 2 after k $\geq$ 10. In other words, we used only the samples collected in the last step of the algorithm. The learning parameters used in our algorithm are k_max = 10, a = 0.4, and b = 0.14 (see Equation 10). We used an empirically determined value of the threshold $\theta$ = 0.04 (Section 3.3). We only change the CPT tables of the parents of a special evidence node A to uniform distributions when Pr(A = a) < 1/(2 ^. n_A). Some of the parameters are a matter of design decision (e.g., the number of samples in our tests), others were chosen empirically. Although we have found that these parameters may have different optimal values for different Bayesian networks, we used the above values in all our tests of the AIS-BN algorithm described in this paper. Since the same set of parameters led to spectacular improvement in accuracy in all tested networks, it is fair to say that the superiority of the AIS-BN algorithm to the other algorithms is not too sensitive to the values of the parameters.

For the SIS algorithm, w^k = 1 by the design of the algorithm. We used l = 2, 500. The updating function in Step 7 of Figure 1 is that of [Shwe et al.1991,Cousins et al.1993]:

Pr_new^k(x_i|pa(X_i),$$\bf e$$) = $${\frac{{\mbox{\rm Pr}}(x_i\vert{{\mbox{\rm pa}}}(X_i)) + k\cdot ... ...\rm Pr}}}_{\mbox{\it current}} (x_i\vert{{\mbox{\rm pa}}}(X_i),{\bf e})}{1+k}}$$  ,

where Pr(x_i|pa(X_i)) is the original sampling distribution, $\widehat{{\mbox{\rm Pr}}}_{\mbox{\it current}}^{}$(x_i|pa(X_i),$\bf e$) is an equivalent of our ICPT tables estimator based on all currently available information, and k is the updating step.