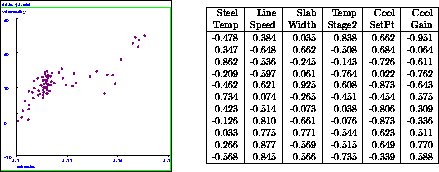
Figure 1: A univariate (left) and a multi-variate (right) data set
As computers and their networks become more prevalent throughout industry, more and more data is becoming available about all aspects of business. Examples of this data include process data from manufacturing or other control systems, inventory data, customer records, marketing and finance data, and product development test data. Locally Weighted Learning and Vizier are all about using this data to make better decisions.
Fig. 1 shows some examples of data. Much of this tutorial will focus on 1 dimensional data because it is easiest to visualize, but all of the software is designed to operate on, and is most useful on, multi-dimensional data. We assume that the relationships between the various attributes may be non-linear and that the data may have significant noise in it. There are many questions we might like to answer with the help of the data and LWL:
In this tutorial we show how to answer these questions and many others using LWL and some data. The tutorial covers three main topics. Sections 1 through 7 describe what a locally weighted model is and the tradeoffs involved in choosing various kinds of locally weighted models. Section 8 discusses methods of automatically finding a good locally weighted model. Section 9 gives examples of how a locally weighted model can be used to make better decisions and answer the questions listed above.
In this tutorial, we refer to a single data point, and a data set, as containing input attributes and output attributes. We are usually given a set of values for the input attributes and asked to estimate things about the corresponding output attributes, or given a desired property in the output attributes and asked to find the input attributes which are estimated to produce the desired output properties. We will assume that the attributes are already labeled as input or output, but there is no problem with changing the labels of attributes in order to investigate various possible relationships. In equations, the input attributes will often be referred to as x, and the output attributes as y.