Introduction to Mechanisms
Yi Zhang
with
Susan Finger
Stephannie Behrens
Linkage are composed of links and
lower pairs. The simplest
closed-loop linkage is the four-bar linkage, which has three moving
links, one fixed link and four pin joints. A linkage with one link
fixed is a mechanism. You can load the following four-bar
linkage into SimDesign from the file mechanisms/fourbar.sim.
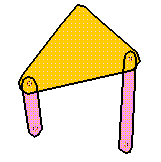
This mechanism has three moving links. Two of them are pinned to
the frame, which is not shown in this picture. In SimDesign, you can
nail these two links to the background.
How many degrees of freedom
(DOF) does this mechanism have? If it has one, you can impose one
constraint on the mechanism for it to have definite motion. For
example, you can pull the nailed link on the left (making it the
input link) and it will turn around the nail. The right link
(now the output link) will make an oscillating motion. Suppose
you put a pen on the top of the triangle-shaped link. (The triangle
is also called a link. A link is not necessarily a simple line-shaped
body). The pen will trace its path. The triangle-shaped link connects
the two moving pivots and couples the input and the output motion;
hence, it is called coupler.
Linkages have different functions. The functions are classified
depending on the primary goal of the mechanism:
- Function generation: the relative motion between the links
connected to the frame,
- Path generation: the path of a tracer point, or
- Motion generation: the motion of the coupler link.
An application of path generation is a crane in which an approximate
horizontal trace is needed.
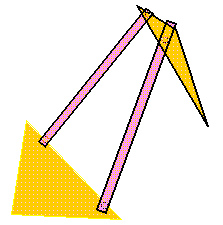
An example of motion generation is a hood which opens and closes.

In a parallelogram four-bar linkage,
the orientation of the coupler does not change during the motion.
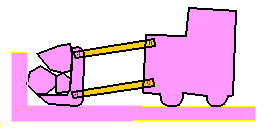
The figure illustrates a loader.
The four-bar mechanism has some special configurations created by
making one or more links infinite in length. The slider-crank (or crank and
slider) mechanism shown below is a four-bar linkage with a slider replacing
an infinitely long output link.
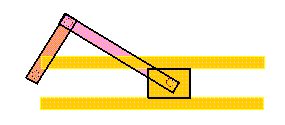
Pull the crank of this mechanism and you will see that it transfers
rotary motion into translation. Most mechanisms are driven by motors,
and slider-cranks are often used to transform rotary motion into
linear motion.
You can also use the slider as the input link and the crank as
the output link. In this case, the mechanism transfers
translational motion into rotary motion. The pistons and crank in an internal
combustion engine are an example of this type of mechanism. The corresponding
SimDesign file is
mechanisms/combustion.sim.
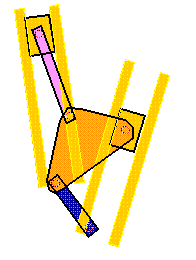
You might wonder why there is another slider and a link on the
left. This mechanism has two
dead points. The
slider and link on the left help the mechanism to overcome these dead
points.
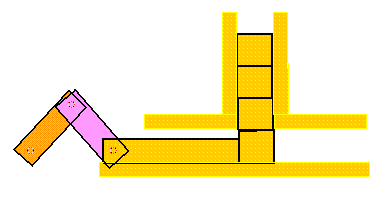
One interesting application of slider-crank is the block
feeder. The SimDesign file can be found in
mechanisms/block.feeder.sim
Linkages, while useful, cannot achieve all possible motions. For
example, if the output link must remain stationary for a
certain period of time while the input link keeps turning, linkages
cannot be used. Cam mechanisms can realize any required output
motion. The composition of a cam mechanisms is simple: a cam, a
follower and a frame. (You may find springs used in a cam mechanism to
keep the follower and the cam in contact, but it is not part of the
cam mechanism.)
 If you turn the cam, the follower will move. The weight of the
follower keeps them in contact. This is called a gravity
constraintcam.
If you turn the cam, the follower will move. The weight of the
follower keeps them in contact. This is called a gravity
constraintcam.
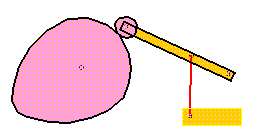
The SimDesign file is mechanisms/cam.oscillating.sim. Notice
that a
roller is used at the end of the follower. In addition, a spring is
used to maintain the contact of the cam and the roller.
If you try to calculate the degrees of
freedom (DOF) of the mechanism, you must imagine that the roller
is welded onto the follower because turning the roller does not
influence the motion of the follower.
There are many kinds of gears. The
following examples are involute spur gears. We use the word
involute because the contour of gear teeth curves inward.
There are many terminologies, parameters and principles for gears.
One of the important concept is the velocity ratio, which is
the ratio of the rotary velocity of the driver gear to that of the
driven gears.

The number of teeth in these gears
are 15 and 30, respectively. If the 15-tooth gear is the driving gear
and the 30-teeth gear is the driven gear, their velocity ratio is 2.
An example of a set of gears is in mechanisms/gear10.30.sim.
When the number of teeth of a gear becomes infinite, the center of
the gear goes to infinity. The gear becomes a rack. The following
picture shows a rack and pinion. The corresponding SimDesign file is
mechanisms/gear.rack.sim.

You can pull the pinion so that it turns and drives the rack. You
can also pull the rack along the guide and drive the pinion.
Gear trains consist of two or more gears that transmit motion from
one axis to another. Ordinary gear trains have axes, relative to the
frame, for all gears comprising the train.


The SimDesign file is mechanisms/gear.planet.sim. Since the sun
gear
(the largest gear) is fixed, the DOF of the above mechanism is one.
When you pull the arm or the planet, the mechanism has a definite
motion. If the sun gear isn't frozen, the relative motion is
difficult to control.
A wheel with suitably shaped teeth, receiving an intermittent circular
motion from an oscillating member, is a
ratchet wheel. The figure below shows a simple ratchet
mechanism.
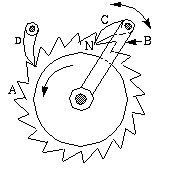
A is the ratchet wheel, and B is an oscillating link. Attached to B
is a pawl which is a link designed to engage with the ratchet
teeth to prevent the wheel from moving in one direction. This
mechanism has a supplementary pawl at D. When the link B moves in a
counterclockwise direction, the pawl C pushes the wheel through a
partial rotation.
When the link B moves clockwise, the pawl C slides over the points of
the teeth while the wheel remains at rest because of the fixed pawl D.
The amount of backward motion possible varies with the pitch of the
teeth. The smaller the teeth, the smaller the backward motion. The
contact surfaces of wheel and pawl should be inclined so they
don't disengage under pressure.

The corresponding SimDesign file is mechanisms/ratchet.sim. The
four-bar linkage on the right generates an oscillating rotation for
link B. Pull the crank to watch the ratchet work.
An interesting example of intermittent gearing is the Geneva Wheel.
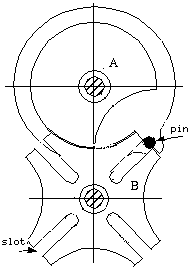
In this mechanism, for every turn of the driver wheel A, the driven
wheel B makes a quarter turn. The pin, attached to driver wheel A,
moves in the slots causing the motion of wheel B. The contact between
the lower part of driver A with the corresponding hollow part of wheel
B, retains it in position when the pin is out of the slot. Wheel A is
cut away near the pin as shown, in order to provide clearance for
wheel B as it moves. If one of the slots is closed, A can make less
than one revolution in either direction before the pin strikes the
closed slot, stopping the motion. Early watches, music boxes, etc.,
used Geneva wheels to prevent over winding. From this application,
they also are called Geneva Stops. As a stop, wheel A is fastened to
the spring shaft, and B turns on the axis of the spring barrel. The
number of slots in B depends upon the number of times the spring shaft
should be turned.
The SimDesign file for Geneva wheel is "geneva.sim".

You may try this mechanism by pulling on the Geneva wheel.
Complete Table of Contents




sfinger@ri.cmu.edu
| 
