Introduction to Mechanisms
Yi Zhang
with
Susan Finger
Stephannie Behrens
Gears are machine elements that transmit motion by means of
successively engaging teeth. The gear teeth act like small levers.
Gears may be classified according to the relative position of the
axes of revolution. The axes may be
- parallel,
- intersecting,
- neither parallel nor intersecting.
Here is a brief list of the common forms. We will discuss each
in more detail later.
Gears for connecting parallel shafts
- Spur gears
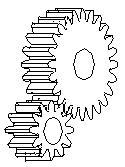
The left pair of gears makes external contact, and the right pair
of gears makes internal contact
-
Parallel helical gears
- Herringbone gears (or double-helical gears)

- Rack and pinion (The rack is like a gear whose
axis is at infinity.)

Gears for connecting intersecting shafts
- Straight bevel gears

- Spiral bevel gears
Neither parallel nor intersecting shafts
- Crossed-helical gears

- Hypoid gears
- Worm and wormgear

Figure 7-2 shows two mating gear teeth,
in which
- Tooth profile 1 drives tooth
profile 2 by acting at the instantaneous contact point K.
- N1N2 is the common normal of the two profiles.
- N1 is the foot of the perpendicular from
O1 to N1N2
- N2 is the foot of the perpendicular from
O2 to N1N2.
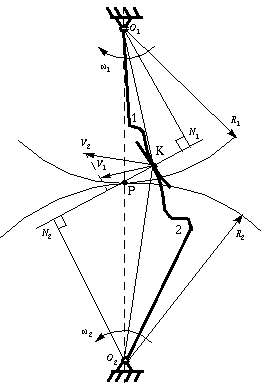
Figure 7-2 Two gearing tooth profiles
Although the two profiles have different velocities
V1 and V2 at point
K, their velocities along N1N2 are
equal in both magnitude and direction. Otherwise the two tooth
profiles would separate from each other. Therefore, we have
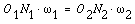 (7-1)
(7-1)
or
 (7-2)
(7-2)
We notice that the intersection of the tangency
N1N2 and the line of center
O1O2 is point P, and
 (7-3)
(7-3)
Thus, the relationship between the angular velocities of the driving
gear to the driven gear, or velocity ratio, of a pair of mating
teeth is
 (7-4)
(7-4)
Point P is very important to the velocity ratio, and it is
called the pitch point. Pitch point divides the line between
the line of centers and its position decides the velocity ratio of the
two teeth. The above expression is the fundamental law of
gear-tooth action.
For a constant velocity ratio, the position of P should remain
unchanged. In this case, the motion transmission between two gears is
equivalent to the motion transmission between two imagined slipless
cylinders with radius R1 and R2 or
diameter D1 and D2. We can get two
circles whose centers are at O1 and
O2, and through pitch point P. These two
circle are termed pitch circles. The velocity ratio is equal to
the inverse ratio of the diameters of pitch circles. This is the
fundamental law of gear-tooth action.
The fundamental law of gear-tooth action may now also be stated
as follow (for gears with fixed center distance) (Ham 58):
The common normal to the tooth profiles at the point of contact must
always pass through a fixed point (the pitch point) on the line of
centers (to get a constant velocity ration).
To obtain the expected velocity ratio of two tooth profiles,
the normal line of their profiles must pass through the corresponding
pitch point, which is decided by the
velocity ratio. The two profiles which satisfy this requirement
are called conjugate profiles. Sometimes, we simply termed the
tooth profiles which satisfy the fundamental law of gear-tooth
action the conjugate profiles.
Although many tooth shapes are possible for which a mating tooth could
be designed to satisfy the fundamental law, only two are in general
use: the cycloidal and involute profiles. The involute
has important advantages -- it is easy to manufacture and the center
distance between a pair of involute gears can be varied without
changing the velocity ratio. Thus close
tolerances between shaft locations are not required when using the
involute profile. The most commonly used conjugate tooth curve
is the involute curve
(Erdman & Sandor 84).
The following examples are involute spur gears. We use the word
involute because the contour of gear teeth curves inward.
Gears have many terminologies, parameters and principles. One of the
important concepts is the velocity ratio, which is the ratio of
the rotary velocity of the driver gear to that of the driven gears.

The SimDesign file for these gears is simdesign/gear15.30.sim.
The number of teeth in these gears are 15 and 30, respectively. If
the 15-tooth gear is the driving gear and the 30-teeth gear is the
driven gear, their velocity ratio is 2. Other examples of gears
are in simdesign/gear10.30.sim and
simdesign/gear20.30.sim
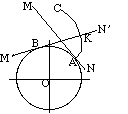
Figure 7-3 Involute curve
The curve most commonly used for gear-tooth profiles is the involute
of a circle. This involute curve is the path traced by a point
on a line as the line rolls without slipping on the circumference of a
circle. It may also be defined as a path traced by the end of a string
which is originally wrapped on a circle when the string is unwrapped
from the circle. The circle from which the involute is derived is
called the base circle.
In Figure 7-3, let line MN roll in the
counterclockwise direction on the circumference of a circle without
slipping. When the line has reached the position M'N', its
original point of tangent A has reached the position K,
having traced the involute curve AK during the motion. As the
motion continues, the point A will trace the involute curve
AKC.
- The distance BK is equal to the arc AB, because
link MN rolls without slipping on the circle.
- For any instant, the instantaneous center of the motion of
the line is its point of tangent with the circle.
Note: We have not defined the term instantaneous center
previously. The instantaneous center or instant center
is defined in two ways (Bradford
& Guillet 43):
- When two bodies have planar relative motion, the instant
center is a point on one body about which the other rotates at the
instant considered.
- When two bodies have planar relative motion, the instant center is
the point at which the bodies are relatively at rest at the instant
considered.
- The normal at any point of an involute is tangent to the base
circle. Because of the property (2) of the involute curve, the motion of
the point that is tracing the involute is perpendicular to the line at any
instant, and hence the curve traced will also be perpendicular to the
line at any instant.
- There is no involute curve within the base circle.
Figure 7-4 shows some of the terms for gears.
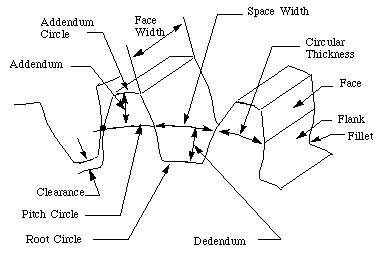
Figure 7-4 Spur Gear
In the following section, we define many of the terms used in the
analysis of spur gears. Some of the terminology has been defined
previously but we include them here for completeness. (See (Ham 58) for more details.)
Table 7-1 lists the standard tooth system
for spur gears. (Shigley &
Uicker 80)
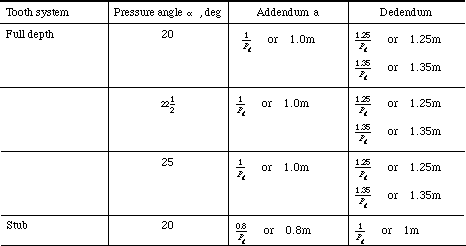
Table 7-1 Standard tooth systems for spur gears
Table 7-2 lists the commonly used diametral pitches.
| Coarse pitch
| 2
| 2.25
| 2.5
| 3
| 4
| 6
| 8
| 10
| 12
| 16
| | Fine pitch
| 20
| 24
| 32
| 40
| 48
| 64
| 96
| 120
| 150
| 200
|
Table 7-2 Commonly used diametral pitches
Instead of using the theoretical pitch circle as an index of tooth size, the base circle, which is a more fundamental circle,
can be used. The result is called the base pitch
pb, and it is related to the circular pitch p
by the equation
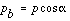 (7-8)
(7-8)
Figure 7-5 shows two meshing gears contacting at
point K1 and K2.
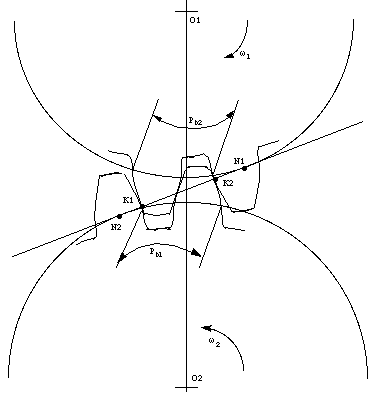
Figure 7-5 Two meshing gears
To get a correct meshing, the distance of
K1K2 on gear 1 should be the same as the
distance of K1K2 on gear 2. As
K1K2 on both gears are equal to the base pitch of their gears, respectively. Hence
 (7-9)
(7-9)
Since
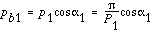 (7-10)
(7-10)
and
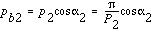 (7-11)
(7-11)
Thus
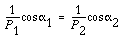 (7-12)
(7-12)
To satisfy the above equation, the pair of meshing gears must satisfy the
following condition:
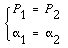 (7-13)
(7-13)
Gear trains consist of two or more gears for the purpose of
transmitting motion from one axis to another. Ordinary gear
trains have axes, relative to the frame, for all gears comprising
the train. Figure 7-6a shows a simple
ordinary train in which there is only one gear for each axis. In
Figure 7-6b a compound ordinary train is
seen to be one in which two or more gears may rotate about a single
axis.
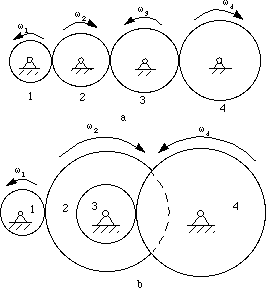
Figure 7-6 Ordinary gear trains
We know that the velocity ratio of a pair of gears is the
inverse proportion of the diameters of their pitch
circle, and the diameter of the pitch circle equals to the number
of teeth divided by the diametral pitch. Also,
we know that it is necessary for the to mating gears to have the same
diametral pitch so that to satisfy the condition of correct
meshing. Thus, we infer that the velocity ratio of a pair of
gears is the inverse ratio of their number of teeth.
For the ordinary gear trains in Figure 7-6a, we have
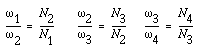 (7-14)
(7-14)
These equations can be combined to give the velocity ratio of the
first gear in the train to the last gear:
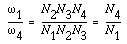 (7-15)
(7-15)
Note:
- The tooth number in the numerator are those of the driven gears,
and the tooth numbers in the denominator belong to the driver
gears.
- Gear 2 and 3 both drive and are, in turn, driven. Thus, they are
called idler gears. Since their tooth numbers cancel, idler
gears do not affect the magnitude of the input-output ratio, but they
do change the directions of rotation. Note the directional arrows in
the figure. Idler gears can also constitute a saving of space and
money (If gear 1 and 4 meshes directly across a long center distance,
their pitch circle will be much larger.)
- There are two ways to determine the direction of the rotary
direction. The first way is to label arrows for each gear as in Figure 7-6. The second way is to multiple
mth power of "-1" to the general velocity ratio. Where
m is the number of pairs of external
contact gears (internal contact gear pairs
do not change the rotary direction). However, the second method cannot
be applied to the spatial gear trains.
Thus, it is not difficult to get the velocity ratio of the gear train
in Figure 7-6b:
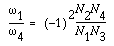 (7-16)
(7-16)
Planetary gear trains, also referred to as epicyclic gear
trains, are those in which one or more gears orbit about the
central axis of the train. Thus, they differ from an ordinary train by
having a moving axis or axes. Figure 7-8 shows a
basic arrangement that is functional by itself or when used as a part
of a more complex system. Gear 1 is called a sun gear , gear
2 is a planet, link H is an arm, or planet
carrier.
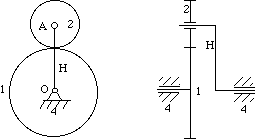
Figure 7-8 Planetary gear trains

Figure 7-7 Planetary gears modeled using SimDesign
The SimDesign file is simdesign/gear.planet.sim. Since the
sun gear (the largest gear) is fixed, the DOF of the above mechanism
is one. When you pull the arm or the planet, the mechanism has a
definite motion. If the sun gear isn't frozen, the relative motion is
difficult to control.
To determine the velocity ratio of the planetary gear trains is slightly more complex an
analysis than that required for ordinary gear
trains. We will follow the procedure:
- Invert the planetary gear train mechanism by imagining the
application a rotary motion with an angular velocity of
 H to the
mechanism. Let's analyse the motion before and after the inversion
with Table 7-3: H to the
mechanism. Let's analyse the motion before and after the inversion
with Table 7-3:
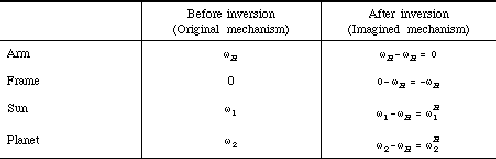
Table 7-3 Inversion of planetary gear trains. Note:  H is the rotary
velocity of gear i in the imagined mechanism. H is the rotary
velocity of gear i in the imagined mechanism.
Notice that in the imagined mechanism, the arm
H is stationary and functions as a frame. No axis of gear moves any
more. Hence, the imagined mechanism is an ordinary
gear train.
- Apply the equation of velocity ratio of the ordinary
gear trains to the imagined mechanism. We get
 (7-17)
(7-17)
or
 (7-18)
(7-18)
Take the planetary gearing train in Figure 7-8
as an example. Suppose N1 = 36, N2 = 18,  1 = 0, 1 = 0,  2 = 30. What is
the value of 2 = 30. What is
the value of  N? N?
With the application of the velocity ratio equation for the planetary
gearing trains, we have the following equation:
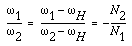 (7-19)
(7-19)
From the equation and the given conditions, we can get the answer:
 N = 10. N = 10.

Complete Table of Contents
- 1 Physical Principles
- 2 Mechanisms and Simple Machines
- 3 More on Machines and Mechanisms
- 4 Basic Kinematics of Constrained Rigid Bodies
- 5 Planar Linkages
- 6 Cams
- 7 Gears
- 7.1 Gear Classification
- 7.2 Gear-Tooth Action
- 7.2.1 Fundamental Law of Gear-Tooth Action
- 7.2.2 Constant Velocity Ratio
- 7.2.3 Conjugate Profiles
- 7.3 Involute Curve
- 7.3.1 Generation of the Involute Curve
- 7.3.2 Properties of Involute Curves
- 7.4 Terminology for Spur Gears
- 7.5 Condition for Correct Meshing
- 7.6 Ordinary Gear Trains
- 7.6.1 Velocity Ratio
- 7.7 Planetary gear trains
- 7.7.1 Velocity Ratio
- 7.7.2 Example
- 8 Other Mechanisms
- Index
- References




sfinger@ri.cmu.edu
| 

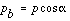


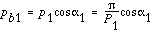
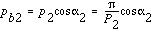
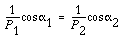
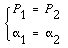

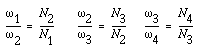
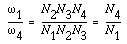
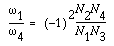
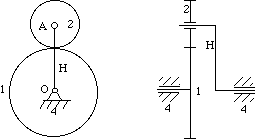

 H to the
mechanism. Let's analyse the motion before and after the inversion
with Table 7-3:
H to the
mechanism. Let's analyse the motion before and after the inversion
with Table 7-3:
 H is the rotary
velocity of gear i in the imagined mechanism.
H is the rotary
velocity of gear i in the imagined mechanism.


 1 = 0,
1 = 0,  2 = 30. What is
the value of
2 = 30. What is
the value of  N?
N?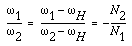
 N = 10.
N = 10. 








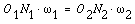









 .
.  :
The angle between the common normal at the point of tooth contact and
the common tangent to the pitch circles. It is also the angle between
the line of action and the common tangent.
:
The angle between the common normal at the point of tooth contact and
the common tangent to the pitch circles. It is also the angle between
the line of action and the common tangent.



