


Next: Optimizing in the Setting
Up: Overview of WIDC
Previous: Building a Large Decision
Schapire  Singer (1998) have investigated classification problems where the aim of the
procedure is not to provide an accurate class for some observation. Rather,
the algorithm outputs a set of values (one for each class) and we expect the
class of the observation to receive the largest value of all, thus being
ranked higher than all others. This approach is particularly useful when
a given example can belong to more than one class (multilabel problems), a case where we expect each of
these classes to receive the greatest values compared to the classes the
examples does not belong to.
Singer (1998) have investigated classification problems where the aim of the
procedure is not to provide an accurate class for some observation. Rather,
the algorithm outputs a set of values (one for each class) and we expect the
class of the observation to receive the largest value of all, thus being
ranked higher than all others. This approach is particularly useful when
a given example can belong to more than one class (multilabel problems), a case where we expect each of
these classes to receive the greatest values compared to the classes the
examples does not belong to.
The ranking loss represents informally the
number of times the hypothesis fails to rank the class of an
example higher than a class to which it does not belong. Before going further, we first generalize our classification setting, and replace the common notation 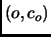 for an example by the more general one
for an example by the more general one  . Here,
. Here,
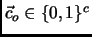 is a vector giving, for each class, the membership to the class (``0'' is no and ``1'' is yes) of the corresponding observation
is a vector giving, for each class, the membership to the class (``0'' is no and ``1'' is yes) of the corresponding observation 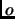 . It is important to note that this setting is more general than the usual Bayesian setting, in which there can exist examples
. It is important to note that this setting is more general than the usual Bayesian setting, in which there can exist examples 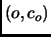 and
and  (using the non-vector notation) for which
(using the non-vector notation) for which 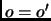 but
but
 . Ranking loss generalizes Bayes to the multilabel problems, and postulates that there can be some examples for which we cannot provide a single class at a time, even if e.g. any of the classes to which the example belongs are susceptible to appear independently later with the same observation.
. Ranking loss generalizes Bayes to the multilabel problems, and postulates that there can be some examples for which we cannot provide a single class at a time, even if e.g. any of the classes to which the example belongs are susceptible to appear independently later with the same observation.
Ranking loss Boosting replaces each example  by a set of
by a set of
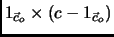 examples, where
examples, where 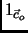 denotes the Hamming weight of
denotes the Hamming weight of  (i.e. the number of classes to which the example belongs). Each of these new examples is denoted
(i.e. the number of classes to which the example belongs). Each of these new examples is denoted 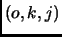 , where
, where 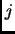 and
and 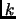 span all values in
span all values in
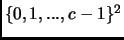 . The distribution of the new examples is renormalized, so that
. The distribution of the new examples is renormalized, so that
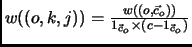 whenever
whenever
![$\vec{c}_o[j]=1$](img86.png) and
and
![$\vec{c}_o[k]=0$](img87.png) , and
, and 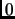 otherwise.
otherwise.
Take some monomial  obtained from the large DC, and all examples satisfying it. We now work with this restricted subset of examples, while calculating the corresponding vector
obtained from the large DC, and all examples satisfying it. We now work with this restricted subset of examples, while calculating the corresponding vector  of
of  . Schapire
. Schapire  Singer (1998) propose a cost function which we should minimize in order to minimize the ranking loss. This function is
Singer (1998) propose a cost function which we should minimize in order to minimize the ranking loss. This function is
Here, 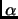 is a tunable parameter which, intuitively, represents the confidence in the choice of
is a tunable parameter which, intuitively, represents the confidence in the choice of 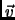 , and leverages its quality. The better
, and leverages its quality. The better 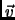 is at classifying examples, the larger is
is at classifying examples, the larger is 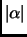 . In our case however, authorizing
. In our case however, authorizing 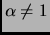 is equivalent to authorizing components for
is equivalent to authorizing components for 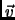 in sets
in sets  for arbitrary
for arbitrary  . To really constrain the components of
. To really constrain the components of 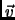 in
in 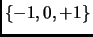 , we have chosen to optimize the criterion
, we have chosen to optimize the criterion
(therefore forcing 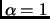 ). Schapire
). Schapire  Singer (1998) conjecture that finding the optimal vector minimizing
Singer (1998) conjecture that finding the optimal vector minimizing 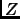 in eq. (2) (which is similar to an oblivious hypothesis according to their definitions), or
in eq. (2) (which is similar to an oblivious hypothesis according to their definitions), or 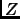 given a particular value of
given a particular value of 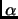 , is
, is 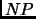 -Hard when
-Hard when 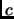 is not fixed, and when the components of
is not fixed, and when the components of 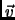 are in the set
are in the set 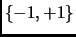 . The following section addresses directly the setting of Schapire
. The following section addresses directly the setting of Schapire  Singer (1998), and presents complexity-theoretic results showing that the minimization of
Singer (1998), and presents complexity-theoretic results showing that the minimization of 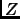 is actually polynomial, but highly complicated to achieve, all the more for what it is supposed to bring to the minimization of
is actually polynomial, but highly complicated to achieve, all the more for what it is supposed to bring to the minimization of 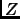 in our setting. A striking result we also give, not related to the purpose of the paper, is that it is actually the maximization of
in our setting. A striking result we also give, not related to the purpose of the paper, is that it is actually the maximization of 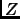 which is
which is 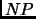 -Hard.
-Hard.
Then, we present the approximation algorithm we have built and implemented to optimize the computation of 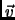 in our setting (components of
in our setting (components of 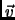 in the set
in the set 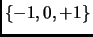 ), along with its properties. While we feel that the ideas used to minimize
), along with its properties. While we feel that the ideas used to minimize 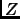 in the setting of Schapire
in the setting of Schapire  Singer (1998) can be adapted to our setting to provide an algorithm that is always optimal, our algorithm has the advantage to be simple, fast, and also optimal for numerous cases. In many other cases, we show that it is still asymptotically optimal as
Singer (1998) can be adapted to our setting to provide an algorithm that is always optimal, our algorithm has the advantage to be simple, fast, and also optimal for numerous cases. In many other cases, we show that it is still asymptotically optimal as 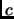 increases.
increases.
Subsections



Next: Optimizing in the Setting
Up: Overview of WIDC
Previous: Building a Large Decision
©2002 AI Access Foundation and Morgan Kaufmann Publishers. All rights reserved.
![$\displaystyle \sum_{o,j,k} {w((o,k,j)) \times e^{-\frac{1}{2}\alpha \left(\vec{v}[j] - \vec{v}[k]\right)}} \:\:.$](img89.png)
![$\displaystyle \sum_{o,j,k} {w((o,k,j)) \times e^{-\frac{1}{2}\left(\vec{v}[j] - \vec{v}[k]\right)}}$](img95.png)