The Complexity of Reasoning with Cardinality Restrictions and Nominals in Expressive Description Logics

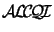
We study the complexity of the combination of the Description Logics $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}}$ and $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ with a terminological formalism based on cardinality restrictions on concepts. 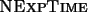These combinations can naturally be embedded into $\ensuremath{C^2}$ , the two variable fragment of predicate logic with counting quantifiers, which yields decidability in $\textsc{NExp\-Time}$ . 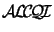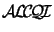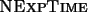We show that this approach leads to an optimal solution for $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ , as $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ with cardinality restrictions has the same complexity as $\ensuremath{C^2}$ ( $\textsc{NExp\-Time}$ -complete). In contrast, we show that for $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}}$ , the problem can be solved in $\textsc{Exp\-Time}$ . This result is obtained by a reduction of reasoning with cardinality restrictions to reasoning with the (in general weaker) terminological formalism of general axioms for $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}}$ extended with nominals . 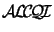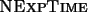Using the same reduction, we show that, for the extension of $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ with nominals, reasoning with general axioms is a $\textsc{NExp\-Time}$ -complete problem. 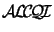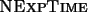Finally, we sharpen this result and show that pure concept satisfiability for $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ with nominals is $\textsc{NExp\-Time}$ -complete. Without nominals, this problem is known to be $\textsc{PSpace}$ -complete.

The Complexity of Reasoning with Cardinality Restrictions and Nominals in Expressive Description Logics

Abstract: