The Logic ALCQI

Definition 2.1 Let N_C be a set of atomic concept names and N_R be a set of atomic role names. Concepts in $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ are built inductively from these using the following rules: all $A \in N_C$ are concepts, and, if C, C₁, and C₂ are concepts, then also

$\begin{displaymath}\neg C, \ C_1 \sqcap C_2, \ \text{and} \ \ensuremath{(\geqslant n \; S \; C)} , \end{displaymath}$

are concepts, where $n \in \mathbb{N}$ and S=R or S= R^-1 for some $R \in N_R$ . A cardinality restriction of $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ is an expression of the form $(\geqslant n \ C)$ or $(\leqslant n \ C)$ where C is a concept and $n \in \mathbb{N}$ ; an $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ - $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ ² is a finite set of cardinality restrictions. The semantics of concepts is defined relative to an interpretation $\mathcal{I} = (\Delta^\mathcal{I},\cdot^\mathcal{I})$ , which consists of a domain $\ensuremath{\Delta^\mathcal{I}}$ and a valuation $(\cdot^\mathcal{I})$ that maps each concept name A to a subset $A^{\mathcal{I}}$ of $\ensuremath{\Delta^\mathcal{I}}$ and each role name R to a subset $R^{\mathcal{I}}$ of $\ensuremath{\Delta^\mathcal{I}}\times \ensuremath{\Delta^\mathcal{I}}$ . This valuation is inductively extended to arbitrary concepts using the following rules, where $\sharp M$ denotes the cardinality of a set M:

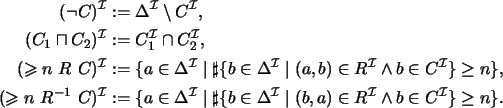
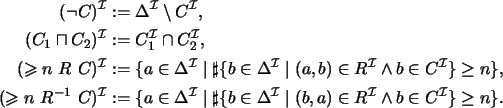
$\begin{align*}(\neg C)^{\mathcal{I}} & := \ensuremath{\Delta^\mathcal{I}}\setmin... ...,a) \in R^{\mathcal{I}} \wedge b \in C^{\mathcal{I}} \} \geq n \}. \end{align*}$

An interpretation $\mathcal{I}$ satisfies a cardinality restriction $(\geqslant n \ C)$ iff $\sharp (C^{\mathcal{I}}) \geq n$ , and it satisfies $(\leqslant n \ C)$ iff $\sharp (C^{\mathcal{I}}) \leq n$ . It satisfies a $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ T iff it satisfies all cardinality restrictions in T; in this case, $\mathcal{I}$ is called a model of T and we will denote this fact by $\mathcal{I}\models T$ . A $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ that has a model is called consistent. With $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}}$ we denote the fragment of $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ that does not contain any inverse roles R^-1.

Using the constructors from Definition 2.1, we use $(\forall \ C)$ as an abbreviation for the cardinality restriction $(\leqslant 0 \; \neg C)$ and introduce the following abbreviations for concepts:

TBoxes consisting of cardinality restrictions have first been studied in [BBH96] for the DL $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}}$ . Obviously, two concepts C,D have the same extension in an interpretation $\mathcal{I}$ iff $\mathcal{I}$ satisfies the cardinality restriction $(\leqslant 0 \ (C \sqcap \neg D) \sqcup (\neg C \sqcap D))$ . Hence, cardinality restrictions can express terminological axioms of the form C = D, which are satisfied by an interpretation $\mathcal{I}$ iff $C^\mathcal{I}= D^\mathcal{I}$ . General axioms are the most expressive TBox formalisms usually studied in the DL context [DL96]. One standard inference service for DL systems is satisfiability of a concept C with respect to a $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ T, i.e., is there an interpretation $\mathcal{I}$ such that $\mathcal{I}\models T$ and $C^\mathcal{I}\neq \emptyset$ . For a TBox formalism based on cardinality restrictions this is easily reduced to TBox consistency, because obviously C is satisfiable with respect to T iff $T \cup \{(\geqslant \ 1 \ C) \}$ is a consistent $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ . For this the reason, we will restrict our attention to $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ consistency; other standard inferences such as concept subsumption can be reduced to consistency as well.

**Figure 2:** The translation from ALCQI into C2
$\begin{figure} \begin{center} \framebox[\textwidth]{ $\begin{array}{l@{\;}c@{... ... \ C) \mid (\bowtie \ n \ C) \in T \} \end{array}$ } \end{center} \end{figure}$

Until now there does not exist a direct decision procedure for $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ consistency. Nevertheless this problem can be decided with the help of a well-known translation of $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ - $\ensuremath {\text {T\hspace {-1pt}}_C\hspace {-1pt}\text {Boxes}}$ to $\ensuremath{C^2}$ [Bor96], given in Figure 2. The logic $\ensuremath{C^2}$ is the fragment of predicate logic in which formulae may contain at most two variables, but which is enriched with counting quantifiers of the form $\exists^{\geq \ell}$ . The translation $\Psi$ yields a satisfiable sentence of $\ensuremath{C^2}$ if and only if the translated $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ is consistent. Since the translation from $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ to $\ensuremath{C^2}$ can be performed in linear time, the $\textsc{NExp\-Time}$ upper bound [GOR97,PST97] for satisfiability of $\ensuremath{C^2}$ directly carries over to $\ensuremath{\mathcal{A}\!\mathcal{L}\!\mathcal{C}\!\mathcal{Q}\!\mathcal{I}}$ - $\ensuremath{\text{T\hspace{-1pt}}_C\hspace{-1pt}\text{Box}}$ consistency:

Please note that the $\textsc{NExp\-Time}$ -completeness result from [PST97] is only valid if we assume unary coding of numbers in the input; this implies that a number n may not be stored in logarithmic space in some k-ary representation but consumes n units of storage. This is the standard assumption made by most results concerning the complexity of DLs. We will come back to this issue in Section 3.3.