- if
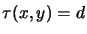 and
and
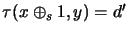 ,
then
,
then
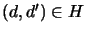 (horizontal constraint);
(horizontal constraint);
- if
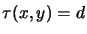 and
and
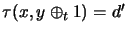 ,
then
,
then
 (vertical constraint);
(vertical constraint);
-
 for
for
 (initial condition).
(initial condition).
Bounded domino systems are capable of expressing the computational behaviour of
restricted, so-called simple, Turing Machines (TM). This restriction is
non-essential in the following sense: Every language accepted in time T(n) and
space S(n) by some one-tape TM is accepted within the same time and space
bounds by a simple TM, as long as
![]() [BGG97].
[BGG97].
Given an initial conditionof length n. Does
tile the torus U(2n+1,2n+1) with initial condition w?
Proof. Let M be a (w.l.o.g. simple) non-deterministic TM with time- (and
hence space-) bound 2n deciding an arbitrary
![]() -complete language
-complete language
![]() over the alphabet
over the alphabet ![]() .
Let
.
Let
![]() be the
according domino system and
be the
according domino system and
![]() the reduction from
Theorem 3.2.
The function
the reduction from
Theorem 3.2.
The function
![]() is a linear reduction from
is a linear reduction from
![]() to
the problem above: For
to
the problem above: For
![]() with |v| = n, it holds that
with |v| = n, it holds that
![]() iff M accepts v in time and space 2|v| iff
iff M accepts v in time and space 2|v| iff
![]() tiles
U(2n+1,2n+1) with initial condition
tiles
U(2n+1,2n+1) with initial condition
![]() .
.