The following movies illustrate the results, obtained with the
relative over-parameterization (ROP) and hybrid conditional
linearization, introduced in the paper. Each solution was computed
with a Kalman Filter; the Boyen-Koller algorithm produces similar
results. In the videos, ellipses denote the 95 per cent
confindence bounds for the camera and object locations. Long
arrows denote the true locations and directions of the cameras.
|
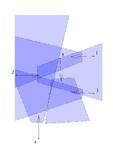
ROP with real cameras: This experiment illustrates the accuracy of our ROP
parameterization. Five real side-facing cameras were instrumented
around a room. A person walked around the room with an LED,
observed by the cameras. The leftmost camera determines the
origin of the coordinate system. When camera 4 observes the
person for the first time at time step 33, it could be located
in a ring around the person; hence the posterior distribution
over its location forms a ring. As the person moves, the
rotational uncertainty of the camera is partially resolved. Our
ROP parameterization allows us to represent these highly
nonlinear distributions with a simple Gaussian. [movie]
|

|
ROP vs. standard parameterization: The following experiment with eight side-facing (1-8) and
four overhead cameras (9-12) compares the accuracy of our ROP
parameterization to the solution obtained with standard absolute
parameterization. Nonlinearities give poor results when camera
poses are represented as x, y, pan.[movie] The ROP
representation, on the other hand, gives excellent results. [movie] Both solutions
employed effective linearization, discussed in the paper. |

|
Closing the loop: The following experiment illustrates the closing of a loop
in a large simulated network of 44 side-facing cameras. As
the person moves around a hallway, the uncertainty in his or
her location accumulates. The uncertainty in the person's
location translates to an uncertainty in the camera locations
at the end of the loop (time steps 130-145). However, the
cameras are tightly correlated with the person as he or she
walks by. Thus, when the person walks into the field of
camera 5 with accurately estimated location, the estimate
person's location becomes more certain, and the accuracy of
the estimates from all the cameras improves. Note that at
convergence, we have accurately estimated the location of all
the cameras. [movie]
|

|
Overhead cameras: The following experiment shows a realistic application of our
approach on a simulated network of 50 overhead cameras. For
overhead cameras at known heights, exactly three degrees of
freedom (x, y, orientation) need to be estimated. As
before, the estimates are very accurate at convergence. Note
that the camera in the center makes a single observation; hence,
the posterior distribution of its location takes on a shape of a
ring, which is correctly represented by our method.
[movie] |

|
Large network of real cameras: The following
experiment shows a realistic application of our approach on a
network of 25 real cameras. The cameras were attached on the
ceiling, facing down, and observe a remote-controlled car,
carrying a color marker. Despite the large number of random
variables in the problem, we can accurately recover the
positions of the cameras online, along with an uncertainty of
the estimates. [movie] |

|
Convergence of the distributed algorithm: This
experiment illustrates the execution of our distributed
algorithm on the network of eight side-facing and four overhead
cameras shown above. In order to condition
on the observations in each time step, the cameras build and
maintain a network junction tree, shown in green. Due
to imperfect communication, the cameras have inconsistent
beliefs about the location of the person (shown by multiple red
ellipses in the video) and of themselves. Nevertheless, they
obtain an accurate solution that is close to the centralized
one. [movie]
|
|
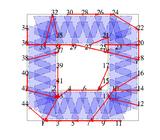
Network partition: The following experiment shows an
execution of our distributed algorithm on a simulated network of
44 side-facing cameras under challenging network conditions. Up
to time step 120, all the cameras can communicate among
themselves, either directly or through their neighbors, and the
observations get propagated to all the cameras in the network.
However, at time step 121, the network is split into two
partitions, and no information about the location of the person
is transmitted from the bottom partition to the top one. This
partitioning is also reflected in the network junction tree,
which is split into two separate trees (shown in red). In the
absence of any observations, cameras 18-38 can only rely on the
weak motion model and become very uncertain of the person's
position. Similarly, when the person closes the loop, the
estimates of cameras 18-38 do not improve. Later, when the
communication is restored, cameras 18-38 improve their estimates
and converge close to the centralized solution. [movie]
|








