 |
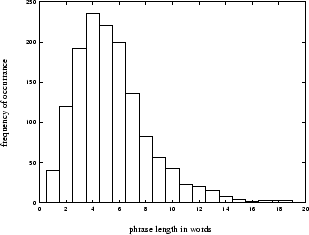
It has been previously noted [Gee and Grosjean, 1983], [Bachenko and Fitzpatrick, 1990], [Wang and Hirschberg, 1992] [Sanders and Taylor, 1995] that phrases occur at somewhat regular intervals and that the likelihood of a break occurring increases with the distance since the last break. The distribution of phrase lengths in words is shown in figure 3. It is clear that the majority of phrases are between 3 and 6 words long.
Previous work has attempted to use this information [Wang and Hirschberg, 1992] [Sanders and Taylor, 1995] but has been hampered by the problem that in a real situation we cannot be certain where the previous break has occurred, and hence it is impossible to reliably compute the distance since the last break. One could simply work in a left to right fashion, placing breaks where they seem most likely and then using that as a definite point to measure the distance to the next hypothesised break. Although simple, this approach is not recommended as a single error cannot be recovered from and may cause errors in all the subsequent decisions. We adopt a different solution, made possible by the use of probabilities throughout the system. Although we can't say when the previous break to juncture ji occurred, we can estimate the probability that a break occurred at any of the previous junctures ji-1, ji-2, ji-3 and thus try to examine all the possibilities.
Instead of explicitly modelling the distance from the last break, we use a n-gram model which gives the probability of all sequences of juncture types in a window of size N. (Note this window is completely separate from the window used in the POS model). N-Grams are the most popular choice of language model in speech recognition systems. The number of possible n-grams is given by TN, where T is the size of the vocabulary. Because of this, speech recognition language models are usually bigrams or trigrams. Here T is the number of juncture types and in our standard system we have a vocabulary of T=2 (break and non-break) and so it is possible to model n-grams as high as 6 and 7 robustly.
The overall goal of the algorithm is to find the most likely sequence of juncture types for the input POS sequence. The probability of a sequence of juncture types (P(J|C)) is calculated using Bayes' Rule by multiplying the POS sequence likelihood by the phrase probability. In principle, the probability of all possible sequences of juncture types is calculated and the highest is chosen. If calculated directly this entails STS possibilities where S is the number of words in the sentence. Even for the case when the juncture types are simply break and non-break (T=2), the number of paths can be very large for long sentences (e.g. over a million for a 20 word sentence) and if the T is larger the number of paths becomes intractable. Instead we use the Viterbi algorithm which finds the most likely path in about T2N calculations. For a detailed explanation see Rabiner and Juang rabiner&juang:94.