| x1 |
|
x | |
| x2 |
|
x | |
|
| |||
| xm |
|
x |
| x1 |
|
x | |
| x2 |
|
x | |
|
| |||
| xm |
|
x |
für
x1 ![]()
![]() p1,...,xm
p1,...,xm ![]()
![]() pm . Sei
vi
pm . Sei
vi ![]()
![]() pi das Inverse zu
pi das Inverse zu
![]() modulo pi
für alle i = 1,...,m , d.h.
modulo pi
für alle i = 1,...,m , d.h.
vi ![]()
![]()
![]() 1
1![]() pi.
pi.
Dann gilt
x ![]()
![]() xi
xi ![]() vi
vi ![]()
![]()
![]() P.
P.
x ![]() xi
xi ![]()
 +
+ ![]()
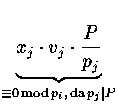
![]() pi
pi
1 < p1 < p2 < ... < pm ![]() m 2
m 2
und
xi = (x![]() pi)
pi)![]() (i = 1,..m)
(i = 1,..m)
x berechnet, korrekt und in NC 1:
NC 1(1) Berechne P : =
pi . NC 1 (2) Berechne
für i = 1,2,...,m parallel. NC 1 (3) Löse die Gleichungen vi
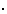

1
pi für i = 1,...,m parallel. (Z.B. durch Ausprobieren) NC 1 (4) Berechne vi
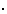
für i = 1,...,m parallel. NC 1 (5) Berechne xi
vi
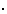
für i = 1,...,m parallel. NC 1 (6) Berechne y : =
xi
vi
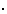

Das gesuchte Ergebnis ist nun
y![]() P = y - t
P = y - t ![]() P, t =
P, t = 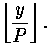
Im folgenden leiten wir uns die Berechnung von t her: Sei k die kleinste Zweierpotenz ![]() m ,
k = 2
m ,
k = 2![]()
![]() m
m![]() .
.
|
| = |
 : s : s | |
|
|
y - s 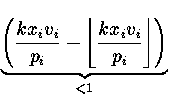 P < P <
| ||
| < |
|
Also gilt sicher:
0 ![]() y -
y - ![]() s
s![]() P < 2P . Damit erhalten wir t wie folgt:
P < 2P . Damit erhalten wir t wie folgt:
1. Fall: y -s
P < P
t =
s
2. Fall: y -
s
P
P
t =
s
+ 1
NC 1(7) Berechne k
vi
xi für i = 1,...,m parallel.
NC 1 (8) Berechne
für i = 1,...,m parallel. Da pi = O(log m) und k
vi
xi = O(log m) genügt ein einfacher Divisionsalgorithmus mit maximal linearer Komplexität (,,any reasonable division circuit``). NC 1 (9) Berechne
. NC 0 (10) Berechne
s
=
(shift right). NC 1 (11) if y -
s
P < P then x : = y -
s
P NC 1 else x : = y -
