Types

   

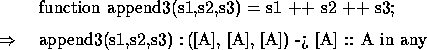
NESL is a strongly typed polymorphic language with a type inference system. Its type system is similar to functional languages such as ML, but since it is first-order (functions cannot be passed as data), function types only appear at the top level. As well as parametric polymorphism NESL also allows a form of overloading similar to what is supplied by the Haskell Language [28].

The type of a polymorphic function in NESL is specified by using type-variables, which are declared in a type-context. For example, the type of the permute function is:

 ([A], [int]) -> [A] :: A in any  

This specifies that for A bound to any type, permute maps a sequence of type [A] and a sequence of type [int] into another sequence of type [A]. The variable A is a type-variable, and the specification A in any is the context. A context can have multiple type bindings separated by semicolons. For example, the zip function, which zips two sequences of equal length together into one sequence of pairs, has type:

 ([A], [B]) -> [(A,B)] :: A in any; B in
any  

User defined functions can also be polymorphic. For example we could define

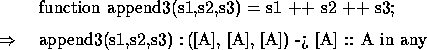
The type inference system will always determine the most general type possible.

 

In addition to parametric polymorphism, NESL supports a form of overloading by including the notion of type-classes. A type-class is a set of types along with an associated set of functions. The functions of a class can only be applied to the types from that class. For example the base types, int and float are both members of the type class number, and numerical functions such as + and * are defined to work on all numbers. The type of a function overloaded in this way, is specified by limiting the context of a type-variable to a specific type-class. For example, the type of + is:

 (A, A) -> A :: A in number  

  
Figure: The type-class hierarchy of NESL. The lower case names are the type classes.

The context ``A in number'' specifies that A can be bound to any member of the type-class number. The fully polymorphic specification any can be thought of as type-class that contains all data types as members. The type-classes are organized into the hierarchy as shown in Figure 4. Functions such as = and < are defined on ordinals, functions such as + and * are defined on numbers, and functions such as or and not are defined on logicals.

User-defined functions can also be overloaded. For example:

It is also possible to restrict the type of a user-defined function by explicitly typing it. For example,

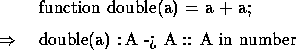
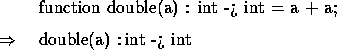
limits the type of double to int -> int. The : specifies that the next form is a type-specifier (see Appendix A for the full syntax of the function construct and type specifiers).

In certain situations the type inference system cannot determine the type even though there is one. For example the function:

 function badfunc(a,b) = a or (a + b);  

will not type properly because or is defined on the type-class logical and + is defined on the type-class number. As it so happens, int is both a logical and an integer, but the NESL inference system does not know how to take intersections of type-classes. In this situation it is necessary to specify the type:

This situation comes up quite rarely.

Specifying the type using ``:'' serves as good documentation for a function even when the inference system can determine the type. The notion of type-classes in NESL is similar to the type-classes used in the Haskell language [28], but, unlike Haskell, NESL\ currently does not permit the user to add new type classes.