A general view of the combinatorial search problem is that it
consists of N
items
and a requirement to find a
solution, i.e., a set of 
items that satisfies specified conditions or
constraints. These conditions in turn can be described as a collection
of nogoods, i.e., sets of items whose
combination is inconsistent with the given conditions. In this context
we define a good to be a set of items that is
consistent with all the constraints of the problem. We also say a set is
complete if it has
L items, while smaller sets are
partial or incomplete. Thus a
solution is a complete good set. In addition, a partial
solution is an incomplete good set.
A key property that makes this set representation conceptually useful is that if a set is nogood, so are all of its supersets. These sets, grouped by size and with each set linked to its immediate supersets and subsets, form a lattice structure. This structure for N=4 is shown in Fig. 1. We say that the
sets of size i are at level i in the lattice. As described below, the various paths through the lattice from levels near the bottom up to solutions, at level L, can be used to create quantum interference as the basis for a search algorithm.
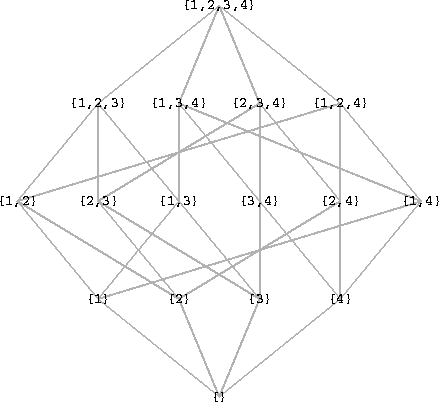
Figure 1: Structure of the set lattice for a problem with four items. The subsets of {1,2,3,4} are grouped into levels by size and lines drawn between each set and its immediate supersets and subsets. The bottom of the lattice, level 0, represents the single set of size zero, the four points at level 1 represent the four singleton subsets, etc.
As an example, consider a problem with N=4 and L=2, and suppose the constraints eliminate items 1 and 3. Then we have the sets {}, {2}, and {4} as partial goods, while {1} and {3} are partial nogoods. Among the 6 complete sets, only {2,4} is good as the others are supersets of {1} or {3} and hence nogood.
For the search problems studied here, the nogoods directly specified by the problem constraints will be small sets of items, e.g., of size two or three. On the other hand, the number of items and the size of the solutions will grow with the problem size. This gives a number of small nogoods, i.e., near the bottom of the lattice. Examples of such problems include binary constraint satisfaction, graph coloring and propositional satisfiability mentioned above.
For CSPs, the items are just the possible variable-value pairs in
the problem. Thus a CSP with n
variables and b values for each has
N=nb items. A solution consists of an
assignment to each variable that satisfies whatever constraints are
given in the problem. Thus a solution consists of a set of
L=n items. In terms of the general framework for
combinatorial search these constraint satisfaction problems will also
contain a number of problem-independent necessary
nogoods, namely those corresponding to giving the same variable two
different values. There are 
such necessary nogoods. For a nontrivial search we
must have 
, so we restrict our attention to the case where
. This requirement is important in allowing the
construction of the quantum search method described below.
Another example is given by a simple CSP consisting of
n=2 variables ( 
and 
) each of which can take on one of b=2 values (1 or 2) and the single constraint that the
two variables take on distinct values, i.e., 
. Hence there are N=nb=4 variable-value pairs 
which we denote as items 1,2,3,4 respectively. The corresponding lattice is given in
Fig. 1. What are the nogoods
for this problem? First there are those due to the explicit constraint
that the two variables have distinct values: 
and 
or {1,3} and {2,4}. In addition, there are necessary nogoods implied by
the requirement that a variable takes on a unique value so that any set
giving multiple assignments to the same variable is necessarily nogood,
namely 
and 
or {1,2} and {3,4}. Referring to Fig. 1, we see that these four nogoods force all sets of size
3 and 4 to be nogood too. However, sets of size zero and one are goods
as are the remaining two sets of size two: {2,3} and {1,4} corresponding to 
and 
which are the solutions to this problem.
Search methods use various strategies for examining the sets in this lattice. For instance, methods such as simulated annealing [32], heuristic repair [39] and GSAT [46] move among complete sets, attempting to find a solution by a series of small changes to the sets. Generally these search techniques continue indefinitely if the problem has no solution and thus they can never show that a problem is insoluble. Such methods are called incomplete. In these methods, the search is repeated, from different initial conditions or making different random choices, until either a solution is found or some specified limit on the number of trials is reached. In the latter case, one cannot distinguish a problem with no solution at all from just a series of unlucky choices for a soluble problem. Other search techniques attempt to build solutions starting from smaller sets, often by a process of extending a consistent set until either a solution is found or no further consistent extensions are possible. In the latter case the search backtracks to a previous decision point and tries another possible extension until no further choices remain. By recording the pending choices at each decision point, these backtrack methods can determine a problem is insoluble, i.e., they are complete or systematic search methods.
This description highlights two distinct aspects of the search procedure: a general method for moving among sets, independent of any particular problem, and a testing procedure that checks sets for consistency with the particular problem's requirements. Often, heuristics are used to make the search decisions depend on the problem structure hoping to identify changes most likely to lead to a solution and avoid unproductive regions of the search space. However, conceptually these aspects can be separated, as in the case of the quantum search algorithm presented below.
