An iterative optimization strategy that appears novel in the clustering literature is iterative hierarchical redistribution. This strategy is rationalized relative to single-observation iterative redistribution: even though moving a set of observations from one cluster to another may lead to a better clustering, the movement of any single observation may initially reduce clustering quality, thus preventing the eventual discovery of the better clustering. In response, hierarchical redistribution considers the movement of observation sets, represented by existing clusters in a hierarchical clustering.
Given an existing hierarchical clustering, a recursive loop examines sibling clusters in the hierarchy in a depth-first fashion. For each set of siblings, an inner, iterative loop examines each sibling, removes it from its current place in the hierarchy (along with its subtree), and resorts the cluster relative to the entire hierarchy. Removal requires that the various counts of ancestor clusters be decremented. Sorting the removed cluster is done based on the cluster's probabilistic description, and requires a minor generalization of the procedure for sorting individual observations: rather than incrementing certain variable value counts by 1 at a cluster to reflect the addition of a new observation, a `host' cluster's variable value counts are incremented by the corresponding counts of the cluster being classified. A cluster may return to its original place in the hierarchy, or as Figure 3 illustrates, it may be sorted to an entirely different location.
Figure 3: Hierarchical redistribution:
the left
subfigure indicates that cluster J has just been removed as a descendent
of D and B, thus producing 
and 
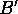, and is about
to be resorted relative to the children of the root (A). The
rightmost figure shows J has been placed as a new child of C.
From Fisher (1995). Figure reproduced with permission from
Proceedings of the First International Conference on Knowledge
Discovery in Data Mining, Copyright © 1995 American
Association for Artificial Intelligence.
The inner loop reclassifies each sibling of a set, and repeats until two consecutive iterations lead to the same set of siblings. The recursive loop then turns its attention to the children of each of these remaining siblings. Eventually, the individual observations represented by leaves are resorted (relative to the entire hierarchy) until there are no changes from one iteration to the next. Finally, the recursive loop may be applied to the hierarchy several times, thus defining an outermost (iterative) loop that terminates when no changes occur from one pass to the next.
There is one modification to this basic strategy that was implemented for reasons of cost: if there is no change in a subtree during a pass of the outermost loop through the hierarchy, then subsequent passes do not attempt to redistribute any clusters in this subtree unless and until a cluster (from some other location in the hierarchy) is placed in the subtree, thus changing the subtree's structure. In addition, there are cases where the PU scores obtained by placing a cluster, C (typically a singleton cluster), in either of two hosts will be the same. In such cases, the algorithm prefers placement of C in its original host if this is one of the candidates with the high PU score. This policy avoids infinite loops stemming from ties in the PU score.
In sum, hierarchical redistribution takes large steps in the search for a better clustering. Similar to macro-operator learners [Iba, 1989] in problem-solving contexts, moving an observation set or cluster bridges distant points in the clustering space, so that a desirable change can be made that would not otherwise have been viewed as desirable if redistribution was limited to movement of individual observations. The redistribution of increasingly smaller, more granular clusters (terminating with individual observations) serves to increasingly refine the clustering.
To a large extent hierarchical redistribution was
inspired by Fisher's [1987a]
COBWEB system, which is fundamentally
a hierarchical-sort-based strategy. However, COBWEB
is augmented by operators of
merging, splitting, and promotion. Merging combines
two sibling clusters in a hierarchical clustering if to do so
increases the quality of the partition of which the clusters
are members; splitting can remove a cluster and promote its
children to the next higher partition; a distinct
promotion operator can
promote an individual cluster to the next higher level.
In fact, these could be regarded as `iterative optimization'
operators, but in keeping with COBWEB's
cognitive modeling motivations,
the cost of applying them is `amortized'
over time: as many observations are sorted, a cluster may migrate
from one part of the hierarchical clustering to another through
the collective and repeated application of merging, splitting, and promotion.
A similar view is expressed by McKusick and Langley [1991],
whose ARACHNE system
differs from COBWEB, in part, by the way that it
exploits the promotion operator.
Unfortunately, in COBWEB, and to a lesser extent in ARACHNE,
merging, splitting,
and promotion are applied locally and migration
through the hierarchy is limited in practice. In contrast,
hierarchical redistribution resorts each cluster, regardless of its
initial location in the tree, through the
root of the entire tree, thus more vigorously pursuing migration
and more globally evaluating the merits of such
moves.
The idea of hierarchical redistribution is also closely related to strategies found in the BRIDGER [Reich & Fenves, 1991] and HIERARCH [Nevins, 1995] systems. In particular, BRIDGER identifies `misplaced' clusters in a hierarchical clustering using a criterion specified, in part, by a domain expert, whereas hierarchical redistribution simply uses the objective function. In BRIDGER each misplaced cluster is removed (together with its subtree), but the cluster/subtree is not resorted as a single unit; rather, the observations covered by the cluster are resorted individually. This approach captures, in part, the idea of hierarchical redistribution, though the resorting of individual observations may not escape local optima to the same extent as hierarchical redistribution.
Given an existing hierarchical clustering and a new observation, HIERARCH conducts a branch-and-bound search through the clustering, looking for the cluster that `best matches' the observation. When the best host is found, clusters in the `vicinity' of this best host are reclassified using branch-and-bound with respect to the entire hierarchy. These clusters need not be singletons, and their reclassification can spawn other reclassifications until a termination condition is reached.
It is unclear how HIERARCH's procedure scales up to large data sets; the number of experimental trials and the size of test data sets is considerably less than we describe shortly. Nonetheless, the importance of bridging distant regions of the clustering space by reclassifying observation sets en masse in made explicit. Like COBWEB, HIERARCH is incremental, changes to a hierarchy are triggered along the path that classifies a new observation, and these changes may move many observations simultaneously, thus `amortizing' the cost of optimization over time. In contrast, hierarchical redistribution is motivated by a philosophy that sorting (or some other method) can produce a tentative clustering over all the data quickly, followed by iterative optimization procedures in background that revise the clustering intermittently. While hierarchical redistribution reflects many of the same ideas implemented in HIERARCH, COBWEB, and related systems, it appears novel as an iterative optimization strategy that is decoupled from any particular initial clustering strategy.
JAIR, 4
