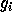The mixture of Gaussians model is a powerful estimation and prediction
technique with roots in the statistics literature
[Titterington
et al. 1985]; it has, over the last few years, been adopted
by researchers in machine learning
[Cheesman et al. 1988, Nowlan 1991, Specht 1991, Ghahramani & Jordan 1994]. The model
assumes that the data are produced by a mixture of N multivariate
Gaussians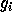 
, for 
(see Figure 1).
In the context of learning from random examples, one begins by
producing a joint density estimate over the input/output space 
based on the training set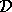 
. The EM algorithm
[Dempster
et al. 1977] can be used to efficiently find a locally optimal fit of
the Gaussians to the data. It is then straightforward to compute
given x by conditioning the joint distribution on x and
taking the expected value.
Figure 1:
Using a mixture of Gaussians to compute 
. The Gaussians model
the data density. Predictions are made by mixing the conditional
expectations of each Gaussian given the input x.
One benefit of learning with a mixture of Gaussians is that there is no fixed distinction between inputs and outputs --- one may specify any subset of the input-output dimensions, and compute expectations on the remaining dimensions. If one has learned a forward model of the dynamics of a robot arm, for example, conditioning on the outputs automatically gives a model of the arm's inverse dynamics. With the mixture model, it is also straightforward to compute the mode of the output, rather than its mean, which obviates many of the problems of learning direct inverse models [Ghahramani & Jordan 1994].
For each Gaussian 
we will denote the input/output means as
and 
and variances and covariances as
, 
and 
respectively.
We can then express the probability of point 
, given 
as
where we have defined
In practice, the true means and variances will be unknown, but can be estimated from data via the EM algorithm. The (estimated) conditional variance of y given x is then
and the conditional expectation 
and variance
given x are:
Here, 
is the amount of ``support'' for the Gaussian 
in the
training data. It can be computed as
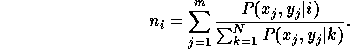
The expectations and variances in Equation 6 are
mixed according to the probability that 
has of being responsible
for x, prior to observing y:
where
For input x then, the conditional expectation
of the resulting mixture and its variance may be written:
where we have assumed that the 
are independent in
calculating 
. Both of these terms can be computed
efficiently in closed form. It is also worth noting that
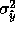is only one of many variance measures we might be
interested in. If, for example, our mapping is stochastically
multivalued (that is, if the Gaussians overlapped significantly in the
x dimension), we may wish our prediction 
to reflect the
most likely y value. In this case, 
would be the mode, and
a preferable measure of uncertainty would be the (unmixed) variance of
the individual Gaussians.
