The conventional view of PCA is a geometric one, finding a low-dimensional projection that minimizes the squared-error loss. An alternate view is a probabilistic one: if the data consist of samples drawn from a probability distribution, then PCA is an algorithm for finding the parameters of the generative distribution that maximize the likelihood of the data. The squared-error loss function corresponds to an assumption that the data is generated from a Gaussian distribution. Collins, Dasgupta & Schapire [CDS02] demonstrated that PCA can be generalized to a range of loss functions by modeling the data with different exponential families of probability distributions such as Gaussian, binomial, or Poisson. Each such exponential family distribution corresponds to a different loss function for a variant of PCA, and Collins, Dasgupta & Schapire [CDS02] refer to the generalization of PCA to arbitrary exponential family data-likelihood models as ``Exponential family PCA'' or E-PCA.
An E-PCA model represents the reconstructed data using a
low-dimensional weight vector ![]() , a basis matrix
, a basis matrix ![]() , and a
link function
, and a
link function ![]() :
:
| (4) |
The link function ![]() is the mechanism through which E-PCA generalizes
dimensionality reduction to non-linear models. For example, the
identity link function corresponds to Gaussian errors and reduces
E-PCA to regular PCA, while the sigmoid link function corresponds to
Bernoulli errors and produces a kind of ``logistic PCA'' for 0-1
valued data. Other nonlinear link functions correspond to other
non-Gaussian exponential families of distributions.
is the mechanism through which E-PCA generalizes
dimensionality reduction to non-linear models. For example, the
identity link function corresponds to Gaussian errors and reduces
E-PCA to regular PCA, while the sigmoid link function corresponds to
Bernoulli errors and produces a kind of ``logistic PCA'' for 0-1
valued data. Other nonlinear link functions correspond to other
non-Gaussian exponential families of distributions.
We can find the parameters of an E-PCA model by maximizing the
log-likelihood of the data under the model, which has been
shown [CDS02] to be equivalent to minimizing a generalized
Bregman divergence
To apply E-PCA to belief compression, we need to choose a link function which accurately reflects the fact that our beliefs are probability distributions. If we choose the link function
Our choice of loss and link functions has two advantages: first, the
exponential link function constrains our low-dimensional
representation
![]() to be positive. Second, our error
model predicts that the variance of each belief component is
proportional to its expected value. Since PCA makes significant
errors close to 0, we wish to increase the penalty for errors in small
probabilities, and this error model accomplishes that.
to be positive. Second, our error
model predicts that the variance of each belief component is
proportional to its expected value. Since PCA makes significant
errors close to 0, we wish to increase the penalty for errors in small
probabilities, and this error model accomplishes that.
If we compute the loss for all ![]() , ignoring terms that depend only on the data
, ignoring terms that depend only on the data ![]() , then6
, then6
The introduction of the link function raises a question: instead of using the complex machinery of E-PCA, could we just choose some non-linear function to project the data into a space where it is linear, and then use conventional PCA? The difficulty with this approach is of course identifying that function; in general, good link functions for E-PCA are not related to good nonlinear functions for application before regular PCA. So, while it might appear reasonable to use PCA to find a low-dimensional representation of the log beliefs, rather than use E-PCA with an exponential link function to find a representation of the beliefs directly, this approach performs poorly because the surface is only locally well-approximated by a log projection. E-PCA can be viewed as minimizing a weighted least-squares that chooses the distance metric to be appropriately local. Using conventional PCA over log beliefs also performs poorly in situations where the beliefs contain extremely small or zero probability entries.
Algorithms for conventional PCA are guaranteed to converge to a unique
answer independent of initialization. In general, E-PCA does not have
this property: the loss function (8) may have multiple
distinct local minima. However, the problem of finding the best
![]() given
given ![]() and
and ![]() is convex; convex optimization problems
are well studied and have unique global
solutions [Roc70]. Similarly, the problem of finding the
best
is convex; convex optimization problems
are well studied and have unique global
solutions [Roc70]. Similarly, the problem of finding the
best ![]() given
given ![]() and
and ![]() is convex. So, the possible local
minima in the joint space of
is convex. So, the possible local
minima in the joint space of ![]() and
and ![]() are highly
constrained, and finding
are highly
constrained, and finding ![]() and
and ![]() does not require solving a
general non-convex optimization problem.
does not require solving a
general non-convex optimization problem.
Gordon [Gor03] describes a fast, Newton's Method approach for
computing ![]() and
and ![]() which we summarize here. This algorithm
is related to Iteratively Reweighted Least Squares, a popular
algorithm for generalized linear regression [MN83]. In
order to use Newton's Method to minimize equation (8), we need its
derivative with respect to
which we summarize here. This algorithm
is related to Iteratively Reweighted Least Squares, a popular
algorithm for generalized linear regression [MN83]. In
order to use Newton's Method to minimize equation (8), we need its
derivative with respect to ![]() and
and ![]() :
:
If we set the right hand side of equation (14) to zero, we can
iteratively compute
![]() , the
, the ![]() column of
column of
![]() , by Newton's method. Let us set
, by Newton's method. Let us set
![]() , and linearize about
, and linearize about
![]() to find roots of
to find roots of ![]() . This gives
. This gives
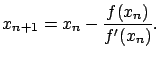 |
(17) |
| (21) |
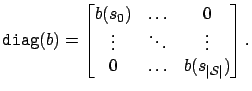 |
(22) |
Combining equation (15) and equation (20), we get
| (23) | |||
| (24) | |||
| (25) |
We now have an algorithm for automatically finding a good low-dimensional
representation
![]() for the high-dimensional belief set
for the high-dimensional belief set
![]() . This algorithm is given in Table 1; the
optimization is iterated until some termination condition is reached, such as
a finite number of iterations, or when some minimum error
. This algorithm is given in Table 1; the
optimization is iterated until some termination condition is reached, such as
a finite number of iterations, or when some minimum error ![]() is
achieved.
is
achieved.
The steps 7 and 9 raise one
issue. Although solving for each row of ![]() or column of
or column of ![]() separately is a convex optimization problem, solving for the two
matrices simultaneously is not. We are therefore subject to potential
local minima; in our experiments we did not find this to be a problem,
but we expect that we will need to find ways to address the local
minimum problem in order to scale to even more complicated domains.
separately is a convex optimization problem, solving for the two
matrices simultaneously is not. We are therefore subject to potential
local minima; in our experiments we did not find this to be a problem,
but we expect that we will need to find ways to address the local
minimum problem in order to scale to even more complicated domains.
Once the bases ![]() are found, finding the low-dimensional
representation of a high-dimensional belief is a convex problem; we
can compute the best answer by iterating equation (26). Recovering a
full-dimensional belief
are found, finding the low-dimensional
representation of a high-dimensional belief is a convex problem; we
can compute the best answer by iterating equation (26). Recovering a
full-dimensional belief ![]() from the low-dimensional representation
from the low-dimensional representation
![]() is also very straightforward:
is also very straightforward:
Our definition of PCA does not explicitly factor the data into ![]() ,
, ![]() and
and
![]() as many presentations do. In this three-part representation of
PCA,
as many presentations do. In this three-part representation of
PCA, ![]() contains the singular values of the decomposition, and
contains the singular values of the decomposition, and ![]() and
and
![]() are orthonormal. We use the two-part representation
are orthonormal. We use the two-part representation
![]() because there is no quantity in the E-PCA decomposition which
corresponds to the singular values in PCA. As a result,
because there is no quantity in the E-PCA decomposition which
corresponds to the singular values in PCA. As a result, ![]() and
and ![]() will not in general be orthonormal. If desired, though, it is possible to
orthonormalize
will not in general be orthonormal. If desired, though, it is possible to
orthonormalize ![]() as an additional step after optimization using conventional
PCA and adjust
as an additional step after optimization using conventional
PCA and adjust ![]() accordingly.
accordingly.