

Next: Learning and inference
Up: Learning and Relevance Bounds
Previous: Learning and Relevance Bounds
The specific method that we will discuss
is from operations research and is used to preprocess mixed integer
programming problems
[Guignard SpielbergGuignard Spielberg1981,SavelsberghSavelsbergh1994].
Suppose that after setting  to true and applying some form of
propagation to our constraint set, we discover that under this
assumption a constraint
to true and applying some form of
propagation to our constraint set, we discover that under this
assumption a constraint 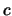 given by
given by
 becomes oversatisfied by an amount
becomes oversatisfied by an amount  in that the sum of the left
hand side is greater (by
in that the sum of the left
hand side is greater (by  ) than the amount required by the right
hand side of the inequality; in the terms of Definition 3.5,
) than the amount required by the right
hand side of the inequality; in the terms of Definition 3.5,
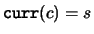 . The oversatisfied constraint
. The oversatisfied constraint 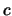 can now be replaced by the
following:
can now be replaced by the
following:
 |
(29) |
If  is true, we know that
is true, we know that
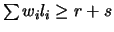 , so
(29) holds. If
, so
(29) holds. If  is false, then
is false, then
 and
we still must satisfy the original constraint
and
we still must satisfy the original constraint
 ,
so (29) still holds. The new constraint implies the
original one, so no information is lost in the replacement.
,
so (29) still holds. The new constraint implies the
original one, so no information is lost in the replacement.
As we have remarked, the OR community uses this technique during
preprocessing. A literal is fixed, propagation is applied, and any
oversatisfied constraint is strengthened. Consider the following set
of clauses:
If we set 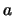 to false, we must then value both
to false, we must then value both 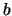 and
and 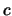 true in
order to satisfy the first two constraints. The third constraint is
now oversatisfied and can thus be replaced by
true in
order to satisfy the first two constraints. The third constraint is
now oversatisfied and can thus be replaced by
The power of this method is that it allows us to build more complex
axioms from a set of simple ones. The strengthened constraint will
often subsume some or all of the constraints involved in generating
it. In this case, the new constraint subsumes all three of the
generating constraints.
Proposition 3.17
Let
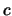
be a constraint and

a partial assignment.
Then if we can conclude that
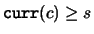
for any solution to
our overall problem that extends

, we can replace
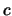
with
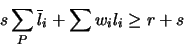 |
(30) |
where the first summation is over literals

.
Proof. For any truth assignment that extends  , (30)
follows from the fact that
, (30)
follows from the fact that
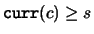 . For any truth assignment
. For any truth assignment
 that does not extend
that does not extend  , there is some
, there is some 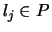 that is false
in
that is false
in  , and so
, and so
Combining this with the original constraint 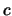 once again produces
(30).
once again produces
(30).



Next: Learning and inference
Up: Learning and Relevance Bounds
Previous: Learning and Relevance Bounds
Matt Ginsberg
2004-02-19
![]() to true and applying some form of
propagation to our constraint set, we discover that under this
assumption a constraint
to true and applying some form of
propagation to our constraint set, we discover that under this
assumption a constraint ![]() given by
given by
![]() becomes oversatisfied by an amount
becomes oversatisfied by an amount ![]() in that the sum of the left
hand side is greater (by
in that the sum of the left
hand side is greater (by ![]() ) than the amount required by the right
hand side of the inequality; in the terms of Definition 3.5,
) than the amount required by the right
hand side of the inequality; in the terms of Definition 3.5,
![]() . The oversatisfied constraint
. The oversatisfied constraint ![]() can now be replaced by the
following:
can now be replaced by the
following:

![]() , (30)
follows from the fact that
, (30)
follows from the fact that
![]() . For any truth assignment
. For any truth assignment
![]() that does not extend
that does not extend ![]() , there is some
, there is some ![]() that is false
in
that is false
in ![]() , and so
, and so