Unit Propagation

Let us begin by discussing propagation techniques in a cardinality or pseudo-Boolean setting.¹¹

A pseudo-Boolean version of unit propagation was first presented by Barth Barth:01 and is described in a number of papers [Aloul, Ramani, Markov, SakallahAloul et al.2002,Dixon GinsbergDixon Ginsberg2000]. In the Boolean case, we can describe a clause as unit if it contains no satisfied literals and at most one unvalued one. To generalize this to the pseudo-Boolean setting, we make the following definition, where we view a partial assignment $P$ simply as the set of literals that it values to true:

Definition 3.5   Let $\sum_i w_i l_i \geq k$ be a pseudo-Boolean clause, which we will denote by $c$. Now suppose that $P$ is a partial assignment of values to variables. We will say that the current value of $c$ under $P$ is given by

$$\mbox{\tt curr}(c,P) = \sum_{\{i\vert l_i\in P\}} w_i - k$$

If no ambiguity is possible, we will write simply $\mbox{\tt curr}(c)$ instead of $\mbox{\tt curr}(c,P)$. In other words, $\mbox{\tt curr}(c)$ is the sum of the weights of literals that are already satisfied by $P$, reduced by the required total weight $k$.

In a similar way, we will say that the possible value of $c$ under $P$ is given by

$$\mbox{\tt poss}(c,P) = \sum_{\{i\vert\neg l_i\not\in P\}} w_i - k$$

If no ambiguity is possible, we will write simply $\mbox{\tt poss}(c)$ instead of $\mbox{\tt poss}(c,P)$. In other words, $\mbox{\tt poss}(c)$ is the sum of the weights of literals that are either already satisfied or not valued by $P$, reduced by the required total weight $k$.¹²

Definition 3.6   Let $c$ be a clause, and $P$ a partial assignment. We will say that $c$ is unit if there is a variable $v$ not appearing in $P$ such that either $P\cup\{v\}$ or $P\cup\{\neg v\}$ cannot be extended to an assignment that satisfies $c$.

In this situation, the variable $v$ is forced to take a value that will help satisfy the clause. This creates a new consequential assignment. Note that if $c$ is already unsatisfiable, we can meet the conditions of the definition by choosing $v$ to be any variable not assigned a value by $P$. Note also that in the pseudo-Boolean case, a clause may actually contain more than one variable that is forced to a specific value. It should be clear that in the Boolean case, this definition duplicates the conditions of the original unit propagation procedure 2.3.

Lemma 3.7   A partial assignment $P$ can be extended in a way that satisfies a clause $c$ if and only if $\mbox{\tt poss}(c,P)\geq 0$.

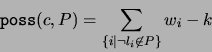
Proof. Assume first that $\mbox{\tt poss}(c,P)\geq 0$, and suppose that we value every remaining variable in a way that helps to satisfy $c$. Having done so, every literal in $c$ that is not currently made false by $P$ will be true, and the resulting value of $c$ will be

$$\sum_{i} w_i l_i = \sum_{\{i\vert\neg l_i \not\in P\}} w_i = \mbox{\tt poss}(c,P) + k \geq k$$

so that $c$ becomes satisfied.

Conversely, suppose that $\mbox{\tt poss}(c,P)<0$. Now the best we can do is still to value the unvalued literals favorably, so that the value of $c$ becomes

$$\sum_{i} w_i l_i = \sum_{\{i\vert\neg l_i \not\in P\}} w_i = \mbox{\tt poss}(c,P) + k < k$$

and $c$ is unsatisfiable.         $\mathchoice{\vcenter{\hrule height.4pt \hbox{\vrule width.4pt height3pt \kern ... ...vrule width.3pt height1.5pt \kern 1.5pt \vrule width.3pt} \hrule height.3pt}}$

Proposition 3.8   A clause $c$ containing at least one unvalued literal is unit if and only if $c$ contains an unvalued literal $l_i$ with weight $w_i > \mbox{\tt poss}(c)$.

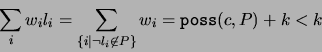
Proof. If there is a literal with weight $w_i > \mbox{\tt poss}(c)$, setting that literal to false will reduce $\mbox{\tt poss}(c)$ by $w_i$, making it negative and thus making the $c$ unsatisfiable. Conversely, if there is no such literal, then $\mbox{\tt poss}(c)$ will remain positive after any single unvalued literal is set, so that $c$ remains satisfiable and is therefore not unit.         $\mathchoice{\vcenter{\hrule height.4pt \hbox{\vrule width.4pt height3pt \kern ... ...vrule width.3pt height1.5pt \kern 1.5pt \vrule width.3pt} \hrule height.3pt}}$

Given the above result, there is little impact on the time needed to find unit clauses. We need simply keep the literals in each clause sorted by weight and maintain, for each clause, the value of $\mbox{\tt poss}$ and the weight of the largest unvalued literal. If we value a literal with different weight, we can apply the test in Proposition 3.8 directly. If we value a literal of the given weight, a short walk along the clause will allow us to identify the new unvalued literal of maximum weight, so that the proposition continues to apply.