

Next: Inference and Resolution
Up: Unit Propagation
Previous: Unit Propagation
Generalizing the idea of watched literals
is no more difficult. We make the following definition:
Definition 3.9
Let
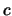
be a clause. A
watching set for 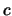
is any set
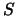
of variables with the property that
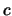
cannot be unit
as long as all of the variables in
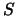
are either unvalued or
satisfied.
Proposition 3.10
Given a clause
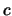
of the form
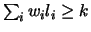
,
let
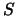
be any set of variables. Then
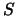
is a watching set for
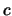
if and only if
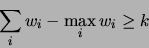 |
(22) |
where the sum and maximum are taken over literals involving variables in
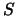
.
Proof. Suppose that all of the variables in 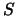 are unvalued or
satisfied. Now let
are unvalued or
satisfied. Now let 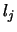 be any unvalued literal in
be any unvalued literal in 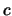 . If
. If
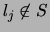 , then
, then
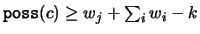 and thus
and thus
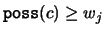 since
since
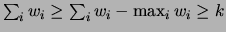 . If, on the other hand,
. If, on the other hand, 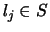 , then
, then
and
Combining these, we get
Either way, we cannot have
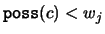 and Proposition 3.8 therefore
implies that
and Proposition 3.8 therefore
implies that 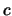 cannot be unit. It follows that
cannot be unit. It follows that 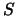 is a watching set.
is a watching set.
The converse is simpler. If
 , value
every literal outside of
, value
every literal outside of 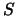 so as to make
so as to make 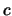 false. Now
false. Now
 , so if
, so if 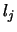 is the literal in
is the literal in 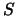 with greatest
weight, the associated weight
with greatest
weight, the associated weight  satisfies
satisfies
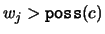 and
and 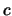 is unit. Thus
is unit. Thus 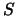 cannot be a watching set.
cannot be a watching set.

This generalizes the definition from the Boolean case, a fact made
even more obvious by:
Corollary 3.11
Given a cardinality constraint
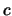
requiring at
least
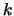
of the associated literals to be true,
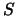
is a watching set
for
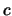
if and only if it includes at least
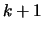
literals in
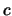
.
Proof. The expression (22) becomes
or


Next: Inference and Resolution
Up: Unit Propagation
Previous: Unit Propagation
Matt Ginsberg
2004-02-19
![]() are unvalued or
satisfied. Now let
are unvalued or
satisfied. Now let ![]() be any unvalued literal in
be any unvalued literal in ![]() . If
. If
![]() , then
, then
![]() and thus
and thus
![]() since
since
![]() . If, on the other hand,
. If, on the other hand, ![]() , then
, then
![]() , value
every literal outside of
, value
every literal outside of ![]() so as to make
so as to make ![]() false. Now
false. Now
![]() , so if
, so if ![]() is the literal in
is the literal in ![]() with greatest
weight, the associated weight
with greatest
weight, the associated weight ![]() satisfies
satisfies
![]() and
and ![]() is unit. Thus
is unit. Thus ![]() cannot be a watching set.
cannot be a watching set.
![]()