

Next: Concluding Remarks
Up: Searching for Bayesian Network
Previous: Comparison with other Approaches
Experimental Results
In this section we shall describe the experiments carried out with our algorithm, the obtained results, and a comparative study with other algorithms for learning Bayesian networks. We have selected nine different problems to test our algorithm, all of which only contain discrete variables: Alarm (Figure 18), Insurance (Figure 19), Hailfinder (Figure 20), Breast-Cancer, crx, Flare2, House-Votes, Mushroom, and Nursery.
The Alarm network displays the relevant variables and relationships for the Alarm Monitoring System [5], a diagnostic application for patient monitoring. This network, which contains 37 variables and 46 arcs, has been considered as a benchmark for evaluating Bayesian network learning algorithms. The input data commonly used are subsets of the Alarm database built by [43], which contains 20000 cases that were stochastically generated using the Alarm network. In our experiments, we have used three databases of different sizes (the first  cases in the Alarm database, for
cases in the Alarm database, for  and
and  ).
).
Figure 18:
The Alarm network
 |
Insurance [6] is a network for evaluating car insurance risks. The Insurance network contains 27 variables and 52 arcs. In our experiments, we have used five databases containing 10000 cases, generated from the Insurance Bayesian network.
Figure 19:
The Insurance network
 |
Hailfinder [1] is a normative system that forecasts severe summer hail in northeastern Colorado. The Hailfinder network contains 56 variables and 66 arcs. In this case, we have also used five databases with 10000 cases generated from the Hailfinder network.
Figure 20:
The Hailfinder network
 |
Breast-Cancer, crx, Flare2, House-Votes, Mushroom, and Nursery are databases available from the UCI Machine Learning Repository. Breast-Cancer contains 10 variables (9 attributes, two of which have missing values, and a binary class variable) and 286 instances. The crx database concerns credit card applications. It has 490 cases and 16 variables (15 attributes and a class variable), and seven variables have missing values. Moreover, six of the variables in the crx database are continuous and were discretized using the MLC++ system [48]. Flare2 uses 13 variables (10 attributes and 3 class variables, one for the number of times a certain type of solar flare occured in a 24-hour period) and contains 1066 instances, without missing values. House-Votes stores the votes for each of the U.S. House of Representatives Congressmen on 16 key votes; it has 17 variables and 435 records and all the variables except two have missing values. Mushroom contains 8124 cases corresponding to species of gilled mushrooms in the Agaricus and Lepiota Family; there are 23 variables (a class variable, stating whether the mushroom is edible or poisonous, and 22 attribute variables) and only one variable has missing values. Nursery contains data relative to the evaluation of applications for nursery schools, and has 9 variables and 12960 cases, without missing values. In all of the cases, missing values are not discarded but treated as a distinct state.
In the first series of experiments, we aim to compare the behavior of our RPDAG-based local search method (RPDAG) with the classical local search in the space of DAGs (DAG). The scoring function selected is BDeu [42] (which is score equivalent and decomposable), with the parameter representing the equivalent sample size set to 1 and a uniform structure prior. The starting point of the search is the empty graph in both cases.
We have collected the following information about the experiments:
- BDeu.-
- The BDeu score (log version) of the learned network.
- Edg.-
- The number of edges included in the learned network.
- H.-
- The Hamming distance, H=A+D+I, i.e. the number of different edges, added (A), deleted (D), or wrongly oriented (without taking into account the differences between equivalent structures) (I), in the learned network with respect to the gold standard network (the original model). This measure is only computed for the three test domains where a gold standard exists.
- Iter.-
- The number of iterations carried out by the algorithm to reach the best network, i.e. the number of operators used to transform the initial graph into a local optimum.
- Ind.-
- The number of individuals (either DAGs or RPDAGs) evaluated by the algorithm.
- EstEv.-
- The number of different statistics evaluated during the execution of the algorithm. This is a useful value to measure the efficiency of the algorithms, because most of the running time of a scoring-based learning algorithm is spent in the evaluation of statistics from the database.
- TEst.-
- The total number of statistics used by the algorithm. Note that this number can be considerably greater than EstEv. By using hashing techniques we can store and efficiently retrieve any previously calculated statistics. It is not therefore necessary to recompute them by accessing the database, thus gaining in efficiency.
- NVars.-
- The average number of variables that intervene in the different statistics (i.e. the values
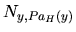 in Eq. (3)) computed. This value is also important because the time required to compute a statistic increases exponentially with the number of variables involved.
in Eq. (3)) computed. This value is also important because the time required to compute a statistic increases exponentially with the number of variables involved.
- Time.-
- The time, measured in seconds, employed by the algorithm to learn the network. Our implementation is written in the JAVA programming language and runs under Linux. This value is only a rough measure of the efficiency of the algorithms, because there are many circumstances that may influence the running time (external loading in a networked computer, caching or any other aspect of the computer architecture, memory paging, use of virtual memory, threading, different code, etc.). Nevertheless, we have tried to ensure that the two algorithms run under the same conditions as far as possible, and the two implementations share most of the code. In fact, the two algorithms have been integrated into the Elvira package (available at http://www.leo.ugr.es/
~elvira).
For the Insurance and Hailfinder domains, the reported results are the average values across the five databases considered. The results of our experiments for synthetic data, i.e. Alarm, Insurance and Hailfinder, are displayed in Tables 3, 4 and 5, respectively, where we also show the BDeu values for the true (
 ) and the empty (
) and the empty (
 ) networks (with parameters re-trained from the corresponding database
) networks (with parameters re-trained from the corresponding database  ), which may serve as a kind of scale. The results obtained for real data are displayed in Table 6.
), which may serve as a kind of scale. The results obtained for real data are displayed in Table 6.
Table 3:
Results for the Alarm databases
| |
BDeu |
Edg |
H |
A |
D |
I |
Iter |
Ind |
EstEv |
TEst |
NVar |
Time |
| Alarm-3000 |
| RPDAG |
-33101 |
46 |
2 |
1 |
1 |
0 |
49 |
63124 |
3304 |
123679 |
2.98 |
111 |
| DAG |
-33109 |
47 |
7 |
3 |
2 |
2 |
58 |
72600 |
3300 |
145441 |
2.88 |
117 |
 |
-33114 |
46 |
|
 |
-59890 |
0 |
|
| Alarm-5000 |
| RPDAG |
-54761 |
46 |
2 |
1 |
1 |
0 |
49 |
62869 |
3326 |
123187 |
2.97 |
179 |
| DAG |
-54956 |
54 |
16 |
9 |
1 |
6 |
60 |
76212 |
3391 |
152663 |
2.93 |
194 |
 |
-54774 |
46 |
|
 |
-99983 |
0 |
|
| Alarm-10000 |
| RPDAG |
-108432 |
45 |
1 |
0 |
1 |
0 |
48 |
61190 |
3264 |
120049 |
2.97 |
346 |
| DAG |
-108868 |
52 |
13 |
7 |
1 |
5 |
60 |
75504 |
3449 |
151251 |
2.94 |
380 |
 |
-108452 |
46 |
|
 |
-199920 |
0 |
|
|
Table 4:
Average results for the Insurance domain across 5 databases of size 10000
| |
BDeu |
Edg |
H |
A |
D |
I |
Iter |
Ind |
EstEv |
TEst |
NVar |
Time |
| RPDAG |
-133071 |
45 |
18 |
4 |
10 |
4 |
48 |
36790 |
1990 |
69965 |
2.95 |
202 |
| DAG |
-133205 |
49 |
25 |
7 |
10 |
8 |
58 |
36178 |
2042 |
72566 |
3.03 |
214 |
 |
-133040 |
52 |
|
 |
-215278 |
0 |
|
|
Table 5:
Average results for the Hailfinder domain across 5 databases of size 10000
| |
BDeu |
Edg |
H |
A |
D |
I |
Iter |
Ind |
EstEv |
TEst |
NVar |
Time |
| RPDAG |
-497872 |
67 |
24 |
12 |
10 |
2 |
68 |
235374 |
7490 |
459436 |
2.92 |
847 |
| DAG |
-498395 |
75 |
45 |
21 |
13 |
11 |
81 |
240839 |
7313 |
482016 |
2.81 |
828 |
 |
-503230 |
66 |
|
 |
-697826 |
0 |
|
|
Table 6:
Results for the UCI databases
| |
BDeu |
Edg |
Iter |
Ind |
EstEv |
TEst |
NVar |
Time |
| Breast-Cancer |
| RPDAG |
-2848 |
6 |
7 |
619 |
151 |
1232 |
2.26 |
0.673 |
| DAG |
-2848 |
6 |
7 |
619 |
148 |
1284 |
2.26 |
0.686 |
| crx |
| RPDAG |
-5361 |
19 |
20 |
5318 |
545 |
10020 |
2.75 |
3.03 |
| DAG |
-5372 |
19 |
20 |
4559 |
510 |
9208 |
2.61 |
2.85 |
| Flare2 |
| RPDAG |
-6728 |
15 |
16 |
2637 |
329 |
4887 |
2.71 |
3.66 |
| DAG |
-6733 |
13 |
14 |
2012 |
310 |
4093 |
2.45 |
3.23 |
| House-Votes |
| RPDAG |
-4629 |
22 |
23 |
6370 |
591 |
11883 |
2.80 |
3.10 |
| DAG |
-4643 |
23 |
24 |
6094 |
621 |
12289 |
2.66 |
3.39 |
| Mushroom |
| RPDAG |
-77239 |
92 |
97 |
43121 |
2131 |
78459 |
3.99 |
432 |
| DAG |
-77208 |
87 |
103 |
39944 |
2173 |
80175 |
3.96 |
449 |
| Nursery |
| RPDAG |
-125717 |
8 |
9 |
415 |
115 |
803 |
2.75 |
11.91 |
| DAG |
-125717 |
8 |
9 |
611 |
133 |
1269 |
2.59 |
13.50 |
|
As we consider there to be a clear difference between the results obtained for the synthetic and the UCI domains, we shall discuss them separately.
- For the synthetic domains (Tables 3, 4 and 5):
- Our RPDAG-based algorithm outperforms the DAG-based one with respect to the value of the scoring function used to guide the search: we always obtain better results on the five databases considered. Note that we are using a logarithmic version of the scoring function, so that the differences are much greater in a non-logarithmic scale. These results support the idea that RPDAGs are able to find new and better local maxima within the score+search approach for learning Bayesian networks in this type of highly structured domains.
- Our search method is also preferable from the point of view of the Hamming distances, which are always considerably lower than the ones obtained by using the DAG space.
- Moreover, our search method is generally more efficient: it carries out fewer iterations (on the five cases), evaluates fewer individuals (on four cases), computes fewer different statistics from the databases (on three cases), uses fewer statistics (on the five cases), and runs faster (on four cases). On the contrary, the average number of variables involved in the statistics is slightly greater (on four cases).
- For the UCI domains (Table 6):
- The results in this case are not as conclusive about the advantages of the RPDAG-based method with respect to the DAG-based one in terms of effectiveness: both algorithms reach the same solution on two cases from six, RPDAG is better than DAG on three cases, and DAG is better on one case.
- With respect to the efficiency of the two algorithms, the situation is similar: neither algorithm clearly outperforms the other with respect to any of the five efficiency measures considered.
In a second series of experiments, we aim to test the behavior of the search in the RPDAG space when used in combination with a search heuristic which is more powerful than a simple greedy search. The heuristic selected is Tabu Search [40,9], which tries to escape from a local maximum by selecting a solution that minimally decreases the value of the scoring function; immediate re-selection of the local maximum just visited is prevented by maintaining a list of solutions that are forbidden, the so-called tabu list (although for practical reasons the tabu list stores forbidden operators not solutions, and consequently, solutions which have not been visited previously may also become forbidden).
We have implemented two simple versions of tabu search: TS-RPDAG and TS-DAG, which explore the RPDAG and DAG spaces, respectively, using the same operators as their respective greedy versions. The parameters used by these algorithms are the length  of the tabu list and the number
of the tabu list and the number  of iterations required to stop the search process. In our experiments, these values have been fixed as follows:
of iterations required to stop the search process. In our experiments, these values have been fixed as follows:  and
and  ,
,  being the number of variables in the domain. The scoring function and the initial graph are the same as in previous experiments, as well as the collected performance measures, with one exception: as the number of iterations is now fixed (Iter=
being the number of variables in the domain. The scoring function and the initial graph are the same as in previous experiments, as well as the collected performance measures, with one exception: as the number of iterations is now fixed (Iter= ), we compute the iteration where the best graph was found (BIter) instead. The results of these experiments are displayed in Tables 7, 8, 9 and 10.
), we compute the iteration where the best graph was found (BIter) instead. The results of these experiments are displayed in Tables 7, 8, 9 and 10.
Table 7:
Results for the Alarm databases using Tabu Search
| |
BDeu |
Edg |
H |
A |
D |
I |
BIter |
Ind |
EstEv |
TEst |
NVar |
Time |
| Alarm-3000 |
| TS-RPDAG |
-33101 |
46 |
2 |
1 |
1 |
0 |
48 |
1779747 |
9596 |
3044392 |
3.63 |
286 |
| TS-DAG |
-33115 |
51 |
11 |
7 |
2 |
2 |
129 |
1320696 |
8510 |
2645091 |
3.59 |
391 |
| Alarm-5000 |
| TS-RPDAG |
-54761 |
46 |
2 |
1 |
1 |
0 |
48 |
1779579 |
10471 |
3031966 |
3.61 |
421 |
| TS-DAG |
-54762 |
47 |
3 |
2 |
1 |
0 |
720 |
1384990 |
11113 |
2773643 |
3.58 |
541 |
| Alarm-10000 |
| TS-RPDAG |
-108432 |
45 |
1 |
0 |
1 |
0 |
47 |
1764670 |
10671 |
3020165 |
3.66 |
735 |
| TS-DAG |
-108442 |
50 |
6 |
5 |
1 |
0 |
284 |
1385065 |
11014 |
2773795 |
3.60 |
862 |
|
Table 8:
Average results for the Insurance domain using Tabu Search
| |
BDeu |
Edg |
H |
A |
D |
I |
BIter |
Ind |
EstEv |
TEst |
NVar |
Time |
| TS-RPDAG |
-133070 |
45 |
18 |
4 |
10 |
4 |
58 |
458973 |
2823 |
751551 |
3.44 |
182 |
| TS-DAG |
-132788 |
47 |
18 |
5 |
10 |
3 |
415 |
352125 |
5345 |
706225 |
4.16 |
428 |
|
Table 9:
Average results for the Hailfinder domain using Tabu Search
| |
BDeu |
Edg |
H |
A |
D |
I |
BIter |
Ind |
EstEv |
TEst |
NVar |
Time |
| TS-RPDAG |
-497872 |
67 |
24 |
12 |
10 |
2 |
67 |
9189526 |
19918 |
1.5223387E7 |
4.07 |
3650 |
| TS-DAG |
-498073 |
70 |
35 |
17 |
13 |
5 |
1631 |
7512114 |
22184 |
1.5031642E7 |
4.07 |
4513 |
|
Table 10:
Results for the UCI databases using Tabu Search
| |
BDeu |
Edg |
BIter |
Ind |
EstEv |
TEst |
NVar |
Time |
| Breast-Cancer |
| TS-RPDAG |
-2848 |
6 |
6 |
8698 |
345 |
14209 |
3.03 |
1.96 |
| TS-DAG |
-2848 |
6 |
6 |
6806 |
316 |
13892 |
2.87 |
1.98 |
| crx |
| TS-RPDAG |
-5361 |
19 |
19 |
61175 |
908 |
98574 |
3.20 |
9.26 |
| TS-DAG |
-5362 |
20 |
29 |
44507 |
1176 |
89714 |
3.17 |
12.23 |
| Flare2 |
| TS-RPDAG |
-6728 |
15 |
15 |
23363 |
616 |
37190 |
3.47 |
9.70 |
| TS-DAG |
-6726 |
15 |
129 |
18098 |
681 |
36665 |
3.27 |
10.60 |
| House-Votes |
| TS-RPDAG |
-4622 |
24 |
180 |
73561 |
1144 |
121206 |
3.32 |
11.14 |
| TS-DAG |
-4619 |
23 |
252 |
56570 |
1364 |
113905 |
3.29 |
15.30 |
| Mushroom |
| TS-RPDAG |
-77002 |
99 |
495 |
209556 |
4021 |
350625 |
4.83 |
883 |
| TS-DAG |
-77073 |
90 |
450 |
157280 |
3455 |
315975 |
4.57 |
1725 |
| Nursery |
| TS-RPDAG |
-125717 |
8 |
8 |
4352 |
251 |
6525 |
3.09 |
28.05 |
| TS-DAG |
-125717 |
8 |
8 |
3898 |
237 |
7991 |
2.95 |
26.20 |
|
For the synthetic domains, in all the cases, except in one of the insurance databases, the results obtained by TS-RPDAG and RPDAG are the same. This phenomenon also appears for the UCI databases, where only in two databases does TS-RPDAG improve the results of RPDAG. Therefore, the Tabu Search does not contribute significantly to improving the greedy search in the RPDAG space (at least using the selected values for the parameters  and
and  ). This is in contrast with the situation in the DAG space, where TS-DAG improves the results obtained by DAG, with the exception of two UCI databases (equal results) and Alarm-3000 (where DAG performs better than TS-DAG).
). This is in contrast with the situation in the DAG space, where TS-DAG improves the results obtained by DAG, with the exception of two UCI databases (equal results) and Alarm-3000 (where DAG performs better than TS-DAG).
With respect to the comparison between TS-RPDAG and TS-DAG, we still consider TS-RPDAG to be preferable to TS-DAG on the synthetic domains, although in this case TS-DAG performs better on the insurance domain. For the UCI databases, the two algorithms perform similarly: each algorithm is better than the other on two domains, and both algorithms perform equally on the remaining two domains. TS-RPDAG is somewhat more efficient than TS-DAG with respect to running time.
We have carried out a third series of experiments to compare our learning algorithm based on RPDAGs with other algorithms for learning Bayesian networks. In this case, the comparison is only intended to measure the quality of the learned network. In addition to the DAG-based local and tabu search previously considered, we have also used the following algorithms:
- PC [66], an algorithm based on independence tests. We used an independence test based on the measure of conditional mutual information [49], with a fixed confidence level equal to 0.99.
- The K2 search method [20], in combination with the BDeu scoring function (K2). Note that K2 needs an ordering of the variables as the input. We used an ordering consistent with the topology of the corresponding networks.
- Another algorithm, BN Power Constructor (BNPC), that uses independence tests [13,14].
The two independence-based algorithms, PC and BNPC, operate on the space of equivalence classes, whereas K2 explores the space of DAGs which are compatible with a given ordering. We have included the algorithm K2 in the comparison, using a correct ordering and the same scoring function as the RPDAG and DAG-based search methods, in order to test whether our method can outperform the results obtained with a more informed algorithm. The results for the algorithms PC and K2 have been obtained using our own implementations (which are also included in the Elvira software). For BNPC, we used the software package available at http://www.cs.ualberta.ca/~jcheng/bnsoft.htm.
The test domains included in these experiments are Alarm, Insurance, and Hailfinder. In addition to the BDeu values, the number of edges in the learned networks and the Hamming distances, we have collected two additional performance measures:
- BIC.-
- The value of the BIC (Bayesian Information Criterion) scoring function [63] for the learned network. This value measures the quality of the network using maximum likelihood and a penalty term. Note that BIC is also score-equivalent and decomposable.
- KL.-
- The Kullback-Leibler distance (cross-entropy) [49] between the probability distribution,
 , associated to the database (the empirical frequency distribution) and the probability distribution associated to the learned network,
, associated to the database (the empirical frequency distribution) and the probability distribution associated to the learned network,  . Notice that this measure is actually the same as the log probability of the data. We have in fact calculated a decreasing monotonic linear transformation of the Kullback-Leibler distance, because this one has exponential complexity and the transformation can be computed very efficiently:
If
. Notice that this measure is actually the same as the log probability of the data. We have in fact calculated a decreasing monotonic linear transformation of the Kullback-Leibler distance, because this one has exponential complexity and the transformation can be computed very efficiently:
If  is the joint probability distribution associated to a network
is the joint probability distribution associated to a network  , then the KL distance can be written in the following way [22,50]:
, then the KL distance can be written in the following way [22,50]:
 |
(5) |
where  denotes Shannon entropy with respect to the distribution
denotes Shannon entropy with respect to the distribution  for the subset of variables
for the subset of variables  and
and
 is the measure of mutual information between the two sets of variables
is the measure of mutual information between the two sets of variables  and
and  . As the first two terms of the expression above do not depend on the graph
. As the first two terms of the expression above do not depend on the graph  , our transformation consists in calculating only the third term in equation (5). So, the interpretation of our transformation of the Kullback-Leibler distance is: the higher this value is, the better the network fits the data. However, this measure should be handled with caution, since a high KL value may also indicate overfitting (a network with many edges will probably have a high KL value).
, our transformation consists in calculating only the third term in equation (5). So, the interpretation of our transformation of the Kullback-Leibler distance is: the higher this value is, the better the network fits the data. However, this measure should be handled with caution, since a high KL value may also indicate overfitting (a network with many edges will probably have a high KL value).
Although for those algorithms whose goal is to optimize the Bayesian score, BDeu is really the metric that should be used to evaluate them, we have also computed BIC and KL because two of the algorithms considered use independence tests instead of a scoring function.
The results of these experiments are displayed in Table 11. The best value for each performance measure and each database is written in bold, and the second best value in italics.
These results indicate that our search method in the RPDAG space, in combination with the BDeu scoring function, is competitive with respect to other algorithms: only the TS-DAG algorithm, which uses a more powerful (and more computationally intensive) search heuristic in the DAG space, and, to a lesser extent, the more informed K2 algorithm, perform better than RPDAG in some cases. Observe that both TS-DAG and K2 perform better than RPDAG in terms of KL on four cases from five.
Table 11:
Performance measures for different learning algorithms
| |
BDeu |
BIC |
KL |
Edg |
H |
A |
D |
I |
| Alarm-3000 |
| RPDAG |
-33101 |
-33930 |
9.23055 |
46 |
2 |
1 |
1 |
0 |
| DAG |
-33109 |
-33939 |
9.23026 |
47 |
7 |
3 |
2 |
2 |
| TS-DAG |
-33115 |
-33963 |
9.23047 |
51 |
11 |
7 |
2 |
2 |
| PC |
-36346 |
-36691 |
8.06475 |
37 |
10 |
0 |
9 |
1 |
| BNPC |
-33422 |
-35197 |
9.11910 |
43 |
7 |
2 |
5 |
0 |
| K2 |
-33127 |
-34351 |
9.23184 |
46 |
2 |
1 |
1 |
0 |
| Alarm-5000 |
| RPDAG |
-54761 |
-55537 |
9.25703 |
46 |
2 |
1 |
1 |
0 |
| DAG |
-54956 |
-55831 |
9.25632 |
54 |
16 |
9 |
1 |
6 |
| TS-DAG |
-54762 |
-55540 |
9.25736 |
47 |
3 |
2 |
1 |
0 |
| PC |
-61496 |
-61822 |
7.85435 |
38 |
16 |
2 |
10 |
4 |
| BNPC |
-55111 |
-55804 |
9.16787 |
42 |
4 |
0 |
4 |
0 |
| K2 |
-54807 |
-55985 |
9.25940 |
47 |
3 |
2 |
1 |
0 |
| Alarm-10000 |
| RPDAG |
-108432 |
-109165 |
9.27392 |
45 |
1 |
0 |
1 |
0 |
| DAG |
-108868 |
-110537 |
9.27809 |
52 |
13 |
7 |
1 |
5 |
| TS-DAG |
-108442 |
-109188 |
9.27439 |
50 |
6 |
5 |
1 |
0 |
| PC |
-117661 |
-117914 |
8.31704 |
38 |
11 |
1 |
9 |
1 |
| BNPC |
-109164 |
-109827 |
9.18884 |
42 |
4 |
0 |
4 |
0 |
| K2 |
-108513 |
-109647 |
9.27549 |
46 |
2 |
1 |
1 |
0 |
| Insurance |
| RPDAG |
-133071 |
-134495 |
8.38502 |
45 |
18 |
4 |
10 |
4 |
| DAG |
-133205 |
-135037 |
8.39790 |
49 |
25 |
7 |
10 |
8 |
| TS-DAG |
-132788 |
-134414 |
8.41467 |
47 |
18 |
5 |
10 |
3 |
| PC |
-139101 |
-141214 |
7.75574 |
33 |
23 |
0 |
20 |
3 |
| BNPC |
-134726 |
-135832 |
8.21606 |
37 |
26 |
3 |
18 |
5 |
| K2 |
-132615 |
-134095 |
8.42471 |
44 |
10 |
1 |
9 |
0 |
| Hailfinder |
| RPDAG |
-497872 |
-531138 |
20.53164 |
67 |
24 |
12 |
10 |
2 |
| DAG |
-498395 |
-531608 |
20.48503 |
75 |
45 |
21 |
13 |
11 |
| TS-DAG |
-498073 |
-516100 |
20.59372 |
70 |
35 |
17 |
13 |
5 |
| PC |
-591507 |
-588638 |
12.65981 |
49 |
50 |
16 |
33 |
1 |
| BNPC |
-503440 |
-505160 |
20.61581 |
64 |
28 |
12 |
15 |
1 |
| K2 |
-498149 |
-531373 |
20.51822 |
67 |
23 |
12 |
11 |
0 |
|
The fourth series of experiments attempts to evaluate the behavior of the same algorithms on a dataset which is different from the training set used to learn the network. In order to do so, we have computed the BDeu, BIC, and KL values of the network structure learned using a database, with respect to a different database: for the Alarm domain, the training set is the Alarm-3000 database used previously, and the test set is formed by the 3000 next cases in the Alarm database; for both Insurance and Hailfinder, we selected one of the five databases that we have been using as the training set and another of these databases as the test set. The results are shown in Table 12.
We can observe that they are analogous to the results obtained in Table 11, where the same databases were used for training and testing. However, in this case RPDAG also performs better than TS-DAG and K2 in terms of KL. Therefore, the good behavior of our algorithm cannot be attributed to overfitting.
Table 12:
Performance measures for the learning algorithms using a different test set
| |
BDeu |
BIC |
KL |
| Alarm-3000 |
| RPDAG |
-32920 |
-33750 |
9.35839 |
| DAG |
-32938 |
-33769 |
9.35488 |
| TS-DAG |
-32947 |
-33793 |
9.35465 |
| PC |
-36286 |
-36632 |
8.15227 |
| BNPC |
-33309 |
-35051 |
9.23576 |
| K2 |
-32951 |
-34165 |
9.36168 |
| Insurance |
| RPDAG |
-132975 |
-134471 |
8.44891 |
| DAG |
-133004 |
-134952 |
8.44745 |
| TS-DAG |
-132810 |
-134281 |
8.44538 |
| PC |
-140186 |
-143011 |
7.70182 |
| BNPC |
-135029 |
-136125 |
8.23063 |
| K2 |
-132826 |
-134309 |
8.44671 |
| Hailfinder |
| RPDAG |
-497869 |
-531165 |
20.58267 |
| DAG |
-498585 |
-531913 |
20.49730 |
| TS-DAG |
-497983 |
-505592 |
20.55420 |
| PC |
-587302 |
-584939 |
12.68256 |
| BNPC |
-506680 |
-508462 |
20.71069 |
| K2 |
-498118 |
-531356 |
20.57876 |
|
Finally, we have carried out another series of experiments, which aim to compare our RPDAG algorithm with the algorithm proposed by [17], that searches in the CPDAG space. In this case, we have selected the House-Votes and Mushroom domains (which were two of the datasets used by [17]). In order to approximate our experimental conditions to those described in Chickering's work, we used the BDeu scoring function with a prior equivalent sample size of ten, and a structure prior of  , where
, where  is the number of free parameters in the DAG; moreover, we used five random subsets of the original databases, each containing approximately 70% of the total data (304 cases for House-Votes and 5686 for Mushroom). Table 13 displays the average values across the five datasets of the relative improvement of the per-case score obtained by RPDAG to the per-case score of DAG, as well as the ratio of the time spent by DAG to the time spent by RPDAG. We also show in Table 13 the corresponding values obtained by Chickering (using only one dataset) for the comparison between his CPDAG algorithm and DAG.
is the number of free parameters in the DAG; moreover, we used five random subsets of the original databases, each containing approximately 70% of the total data (304 cases for House-Votes and 5686 for Mushroom). Table 13 displays the average values across the five datasets of the relative improvement of the per-case score obtained by RPDAG to the per-case score of DAG, as well as the ratio of the time spent by DAG to the time spent by RPDAG. We also show in Table 13 the corresponding values obtained by Chickering (using only one dataset) for the comparison between his CPDAG algorithm and DAG.
Table 13:
Comparison with Chickering's work on completed PDAGs
| |
RPDAG versus DAG |
CPDAG versus DAG |
|
Relative |
Time |
Relative |
Time |
| Dataset |
Improv. |
Ratio |
Improv. |
Ratio |
| House-Votes |
0.0000 |
1.041 |
0.0000 |
1.27 |
| Mushroom |
0.0158 |
1.005 |
-0.0382 |
2.81 |
|
We may observe that the behavior of RPDAG and CPDAG is somewhat different: although both algorithms are more efficient than DAG, it seems to us that CPDAG runs faster than RPDAG. With respect to effectiveness, both RPDAG and CPDAG obtain exactly the same solution as DAG in the House-Votes domain (no relative improvement); however, in the other domain, RPDAG outperforms DAG (on the five datasets considered) whereas CPDAG performs worse than DAG. In any case, the differences are small (they could be a result of differences in the experimental setup) and a much more systematic experimentation with these algorithms would be necessary in order to establish general conclusions about their comparative behavior.


Next: Concluding Remarks
Up: Searching for Bayesian Network
Previous: Comparison with other Approaches
Luis Miguel de Campos Ibáñez
2003-05-30
![]() cases in the Alarm database, for
cases in the Alarm database, for ![]() and
and ![]() ).
).
![]() ) and the empty (
) and the empty (
![]() ) networks (with parameters re-trained from the corresponding database
) networks (with parameters re-trained from the corresponding database ![]() ), which may serve as a kind of scale. The results obtained for real data are displayed in Table 6.
), which may serve as a kind of scale. The results obtained for real data are displayed in Table 6.
![]() of the tabu list and the number
of the tabu list and the number ![]() of iterations required to stop the search process. In our experiments, these values have been fixed as follows:
of iterations required to stop the search process. In our experiments, these values have been fixed as follows: ![]() and
and ![]() ,
, ![]() being the number of variables in the domain. The scoring function and the initial graph are the same as in previous experiments, as well as the collected performance measures, with one exception: as the number of iterations is now fixed (Iter=
being the number of variables in the domain. The scoring function and the initial graph are the same as in previous experiments, as well as the collected performance measures, with one exception: as the number of iterations is now fixed (Iter=![]() ), we compute the iteration where the best graph was found (BIter) instead. The results of these experiments are displayed in Tables 7, 8, 9 and 10.
), we compute the iteration where the best graph was found (BIter) instead. The results of these experiments are displayed in Tables 7, 8, 9 and 10.
![]() and
and ![]() ). This is in contrast with the situation in the DAG space, where TS-DAG improves the results obtained by DAG, with the exception of two UCI databases (equal results) and Alarm-3000 (where DAG performs better than TS-DAG).
). This is in contrast with the situation in the DAG space, where TS-DAG improves the results obtained by DAG, with the exception of two UCI databases (equal results) and Alarm-3000 (where DAG performs better than TS-DAG).
![]() , where
, where ![]() is the number of free parameters in the DAG; moreover, we used five random subsets of the original databases, each containing approximately 70% of the total data (304 cases for House-Votes and 5686 for Mushroom). Table 13 displays the average values across the five datasets of the relative improvement of the per-case score obtained by RPDAG to the per-case score of DAG, as well as the ratio of the time spent by DAG to the time spent by RPDAG. We also show in Table 13 the corresponding values obtained by Chickering (using only one dataset) for the comparison between his CPDAG algorithm and DAG.
is the number of free parameters in the DAG; moreover, we used five random subsets of the original databases, each containing approximately 70% of the total data (304 cases for House-Votes and 5686 for Mushroom). Table 13 displays the average values across the five datasets of the relative improvement of the per-case score obtained by RPDAG to the per-case score of DAG, as well as the ratio of the time spent by DAG to the time spent by RPDAG. We also show in Table 13 the corresponding values obtained by Chickering (using only one dataset) for the comparison between his CPDAG algorithm and DAG.