Theorem 1
When the size of a DC is measured as its whole number of literals, it is
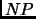
-Hard to find the smallest decision committee consistent with a set of examples
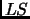
.
Theorem 2
It is
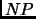
-Hard to find the smallest weighted linear combinations of DT consistent with a set of examples
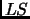
, without limitation on the leveraging coefficients, or for any possible limitation, as long as at least one non-zero value is authorized.