The Size of a DC is Measured as its Number of Rules

We now state and prove the equivalent of Theorem 1 with this new size notion.

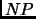
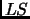
Theorem 3   When the size of a DC is measured as its number of rules, it is $NP$-Hard to find the smallest decision committee consistent with a set of examples $LS$. The result holds even when the concept labeling the examples is a monotone-DNF formula, that is, a disjunction of conjunction (DNF), each without negative literals.

Proof: See the Appendix. $\hbox{\vrule width 0.8pt \vbox to6pt{\hrule depth 0.8pt width 5.2pt \vfill\hrule depth 0.8pt}\vrule width 0.8pt}$
A previous work [Kearns et al.1987] proves a similar theorem concerning the minimization of the size of a DNF. Theorem 3 can be shown to be more general, as the class of DC $_{\{-1,0,+1\}}$ with two rules strictly contains that of DNF with two monomials.
The statement of Theorems 1, 2, 3 as optimization problems was chosen for pure convenience ; replacing them by their associated decision problems (decide whether there exist a consistent formula whose size is no more than some fixed threshold) would trivially make the problems not only $NP$-Hard, but also $NP$-Complete.