Before proving the main result of this section, we show that there is
a schedule of length 
that uses queues of
size 
. This preliminary result is
substantially simpler to prove because of the relaxed bounds on the
schedule length and queue size. Nevertheless, it illustrates the
basic ideas necessary to prove the main result. We begin by proving a
lemma that is used in the proofs of both the preliminary result and
the main result.
Before proceeding, we need to introduce some notation. A T-frame is
a sequence of T consecutive time steps. The frame congestion,
C, in a T-frame is the largest number of packets that traverse any
edge in the frame. The relative congestion, R, in a T-frame
is the ratio 
of the congestion in the frame to the size of the
frame.
Proof: The proof uses the Lovász Local Lemma. The first step is to
assign an initial delay to each packet. Without loss of generality,
we assume that c=d. The delays are chosen from the range 
, where 
is a fixed constant that will be determined later.
In the resulting schedule, 
, a packet that is assigned a delay of
x waits in its initial queue for x steps, then moves on to its
destination without waiting again until it enters its final queue.
The length of 
is at most 
. We use the Lovász
Local Lemma to show that if the delays are chosen randomly,
independently, and uniformly, then with nonzero probability the
relative congestion in any frame of size 
or greater is at
most 1. Thus, such a set of delays must exist.
To apply the Lovász Local Lemma, we associate a bad event with
each edge. The bad event for edge g is that more than T packets
use g in some T-frame, for 
. To show that there is
a way of choosing the delays so that no bad event occurs, we need to
bound the dependence, b, among the bad events and the probability,
p, of each individual bad event occurring.
The dependence calculation is straightforward. Whether or not a bad
event occurs depends solely on the delays assigned to the packets that
pass through the corresponding edge. Thus, two bad events are
independent unless some packet passes through both of the
corresponding edges. Since at most c packets pass through an
edge, and each of these packets passes through at most d other
edges, the dependence, b, of the bad events is at most 
.
Computing the probability of each bad event is a little trickier. Let p be the probability of the bad event corresponding to edge g. Then
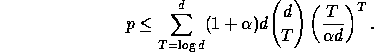
This expression is
derived as follows. Frames of size greater than d cannot have
relative congestion greater than 1, since the total congestion is
only d. Thus, we can ignore them. We bound the probability that
any frame has relative congestion greater than 1 by summing, over
all frame sizes T from 
to d, the probability that some
T-frame has relative congestion greater than 1. Furthermore, for
any T, there are at most 
different T-frames and we
bound the probability that any one of them has relative congestion
greater than 1 by summing their individual probabilities. The
number of packets passing through g in any T-frame has a binomial
distribution. There are d independent Bernoulli trials, one for
each packet that uses g. Since at most T of the possible 
delays will actually send a packet through g in the frame, each
trial succeeds with probability 
. (Here we use the
assumption that the paths are edge-simple.) The probability of more
than T successes is at most 
.
For sufficiently large, but fixed, 
the product 4pb is less
than 1, and thus, by the Lovász Local Lemma, there is some
assignment of delays such that the relative congestion in any frame of
size 
or greater is at most 1.
Proof: For simplicity, we shall assume without loss of generality
that c=d, so that the bounds on the length and queue size are
and 
, respectively.
The proof has the following outline. We begin by using
Lemma 3.2 to produce a schedule 
in which the
number of packets that use an edge in any 
-frame is at most
. Next we break the schedule into 
-frames, as shown in Figure 3. Finally, we view each
-frame as a routing problem with dilation 
and
congestion 
, and solve it recursively.
Figure 3: Schedule 
. The schedule is derived
from the greedy schedule, 
, by assigning an initial delay
in the range 
to each packet. We use the Lovász Local
Lemma to show that within each 
-frame, at most 
packets pass through each edge.
Each 
-frame in 
can be viewed as a separate scheduling
problem where the origin of a packet is its location at the beginning
of the frame, and its destination is its location at the end of the
frame. If at most 
packets use each edge in a 
-frame,
then the congestion of the problem is 
. The dilation is also
because in 
time steps a packet can move a distance
of at most 
. In order to schedule each frame independently, a
packet that arrives at its destination before the last step in the
rescheduled frame is forced to wait there until the next frame begins.
All that remains is to bound the length of the schedule and the size
of the queues. The recursion proceeds to a depth of 
at
which point the frames have constant size, and at most a constant
number of packets use each edge in each frame. The resulting schedule
can be converted to one in which at most one packet uses each edge in
each time step by slowing it down by a constant factor. Since the
length of the schedule increases by a constant factor during each
recursive step, the length of the final schedule is 
.
The bound on the queue size follows from the observation that no
packet waits at any one spot (other than its origin or destination)
for more than 
consecutive time steps, and in
the final schedule at most one packet traverses each edge at each time
step.
