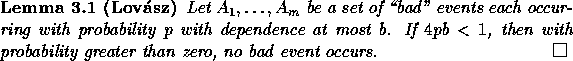In this section, we prove that for any set of packets whose paths are
edge-simple
and have congestion c and dilation d, there is a
schedule of length 
in which at most one packet traverses each
edge of the network at each step, and at most a constant number of
packets wait in each queue at each step. Note that there are no
restrictions on the size, topology, or degree of the network or on the
number of packets.
Our strategy for constructing an efficient schedule is to make a
succession of refinements to the ``greedy'' schedule, 
, in which
each packet moves at every step until it reaches its final
destination. This initial schedule is as short as possible; its
length is only d. Unfortunately, as many as c packets may have to
use an edge at a single time step in 
, whereas in the final
schedule at most one packet is allowed to use an edge at each step.
Each refinement will bring us closer to meeting this requirement by
bounding the congestion within smaller and smaller frames of time.
The proof uses the Lovász Local Lemma [12, pp. 57-58,] at
each refinement step. Given a set of ``bad'' events in a probability
space, the lemma provides a simple inequality which, when satisfied,
guarantees that with probability greater than zero, no bad event
occurs. The inequality relates the probability that each bad event
occurs with the dependence among them. A set of events 
in a probability space has dependence at most b if every
event is mutually independent of some set of m-b-1 other bad events.
The lemma is nonconstructive; for a discrete probability space, it
shows only that there exists some elementary outcome that is not in any
bad event.
