There is a simple randomized on-line algorithm for producing a
schedule of length 
using queues of size 
, where c is the congestion, d is the dilation, and N is
the number of packets.
First, each packet is assigned a delay chosen randomly, independently,
and uniformly from the interval 
,
where 
is a constant that will be specified later. A packet
that is assigned a delay of x waits in its initial queue for x
time steps, and then moves on to its final destination without ever
stopping.
The trouble with this schedule is that several packets may traverse
the same edge in a single step. However, we can bound the number of
packets that are likely to do so. The probability that more than
packets use a particular edge g at a particular time
step t is at most
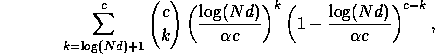
since at most c different packets
pass through g, and for each of these, at most one of the
possible delays sends it through g at
step t. This sum is at most 
. To bound the
probability that more than 
packets pass through any edge
at any time step, we multiply this quantity by the number of choices
for g, at most Nd, and the number of choices for t, at most
. Using the inequality 
for 0 < b < a, and noting that 
, we see
that for large enough, but fixed, 
, the product is at most
. Thus, with high probability, no more than 
packets will want to traverse any edge at any step of this
unconstrained schedule.
Each step of the unconstrained schedule can be simulated by 
steps of a legitimate schedule. The final schedule requires
steps to complete the routing, and uses queues of
size 
.