Nearest neighbor

  
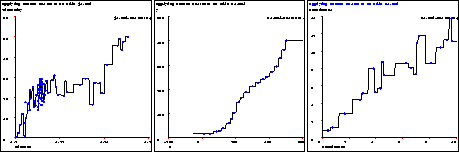
Figure 3: Nearest neighbor on some one dimensional data sets

Another obvious choice for a model is to look for the nearest point in the training data and predict whatever the output was for that point. This method is called nearest neighbor. We can see what it looks like using Vizier. We'll start with the a1.mbl file we've already loaded.

Edit -> Metacode -> Regression A: Averaging
                    Localness  0: No Local Weighting
                    Neighbors  1: T+1 Nearest
Model -> Graph -> Graph

File -> Open -> j1.mbl
Model -> Graph -> Graph

File -> Open -> k1.mbl
Model -> Graph -> Graph

The resulting graphs can be seen in fig. 3. The fit to k1.mbl is not bad, but the others are clearly fitting the noise. In some ways, nearest neighbor is at the opposite end of the spectrum from linear regression. It has little bias (assumptions about what the true function is), which allows it to fit non-linear functions without difficulty. Unfortunately, it suffers from high variance, which means noisy data causes it to make erratic predictions, as can be seen from the graphs. There are several drawbacks to the nearest neighbor method:

• Fitting the noise causes larger prediction errors than if the noise has been filtered out well.

• You can not make estimates of the gradients or the amount of noise since the approximated function is a step function passing through all the data.

• It does not interpolate smoothly between data points.

Generally, the way to overcome the problems listed above is to introduce a model with additional bias (such as assuming the function is relatively smooth). Adding bias can reduce variance which will make the model more robust to noisy data. However, as we saw with linear regression, bias which is based on incorrect assumptions can cause errors as well. The trick is to find a model with bias that will overcome noise and problems from little data (we will discuss this more later), while not causing problems from inability to properly fit the function. Unfortunately, there is no single model which performs well across all data sets. We will see later how Vizier can automatically find a good model for a given data set.