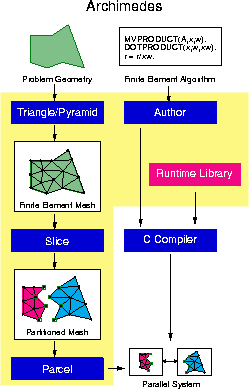
Figure 6: The Archimedes system.
Archimedes [7, 2] is a general-purpose toolset for the efficient mapping of unstructured mesh computations arising from numerical solution of PDEs onto parallel systems. Archimedes is designed to insulate the user from issues of parallelism and communication, and to allow easy and natural expression of unstructured mesh finite element methods and solvers. Its component tools are based on the algorithms for mesh generation, partitioning, and parceling described above. Archimedes also includes a code generator called Author that is targeted to the sorts of computations arising in the solution of PDE problems by unstructured finite element methods [21].
The Archimedes system is depicted in Figure 6.

Figure 6: The Archimedes system.
Input to Archimedes includes (i) the problem geometry, and (ii) a sequential program containing an element-level description of the finite element approximation as well as a high-level description of the solution method. The input program is written in C, augmented with finite element-specific and linear algebraic primitive operations that include vector and matrix assembly, imposition of boundary conditions, sparse matrix-vector products, dot products, and preconditioning. Additional functions are specific to elastic wave propagation, and include absorbing boundaries, damping, and seismic input incorporation. Archimedes programs contain no explicit communication statements, and thus can be written without any knowledge of the parallel machine's underlying communication system. The set of primitives that Archimedes understands is rich enough to express algorithms for solution of linear and nonlinear scalar and vector PDEs, using arbitrary-order finite elements in space and either explicit or implicit methods in time. For implicit methods, the Archimedes language provides for expression of various stationary iterative solvers as well as Krylov subspace methods. Furthermore, users can add new primitives as the need arises.
Triangle [20] is a two-dimensional quality mesh generator in the Archimedes toolset. Triangle operates on a description of the input geometry and produces a two-dimensional triangular mesh with guaranteed angle bounds that satisfies user-specified bounds on element size. These element size bounds can vary spatially, and can be set a priori, based on features of the problem geometry, or a posteriori, within a solution-adaptive scheme. Archimedes also includes a rudimentary three-dimensional mesher, Pyramid. We use Pyramid's Delaunay capability to tetrahedralize the node sets generated by the octree algorithm, as described in Section 3.1. This is sufficient for basin meshes, since the geometry is simple but the physics drives the mesh resolution. Other finite element applications, for example solid mechanics and aerodynamics, will require support for more complex geometries. Extensions to Pyramid to allow for arbitrary geometry are underway. Sequential mesh generation as we have implemented it in Archimedes on the DEC 8400 is adequate for up to 100-200 million tetrahedra. For the largest problems, such as the Greater Los Angeles Basin at a frequency of 2Hz, sequential mesh generation may become a bottleneck. We may parallelize this task in the future.
Archimedes' toolset also includes Slice, an implementation of the asymptotically optimal mesh partitioner [15] discussed in Section 3.2. Once Slice partitions a mesh into subdomains, its output is fed to Parcel, which prepares input for the parallel program. Parcel generates the communication schedule for each processor, the global-to-local mapping information for the mesh nodes and elements, and the local stiffness matrix structure. As with mesh generation, sequential execution (on the DEC 8400) of the mesh partitioning and parceling tasks is sufficiently quick for the large scale problems we target. For problems requiring more than 100-200 million elements, we may have to parallelize partitioning and parceling, more for memory reasons than speed. Unlike meshing, parallelizing these two tasks is relatively straightforward.
The output of Parcel is a single file containing mesh information; this is read by the parallel program. The only program output we are interested in regards free surface displacements and velocities, rather than volume information; thus output is not as significant a problem here as it is in such applications as fluid mechanics. In the interest of portability, we have not yet parallelized I/O. As problem size continues to grow in the future, parallel I/O may become necessary.
Archimedes' parallelizing compiler generates code for any parallel system with C and MPI implementations, including networks of workstations (using the Argonne/Mississippi State MPICH implementation), Intel's Paragon (also using MPICH) and the Cray T3D (using the CRI/EPCC MPI implementation). Finally, Archimedes includes Show Me, an X-Windows based unstructured mesh visualization system. This allows 3D display of nodal distributions, meshes, partitions, communication graphs, and solutions. Such basic capabilities as rotation, shading, zooming, cutaway views, and PostScript output are supported. Figures 2, 3, 4, and 5 were generated by Show Me.
Our decision to build Archimedes was undertaken for several reasons. First, such a system allows application specialists to focus on what they do best: designing numerical methods and concentrating on the physics of the problems at hand. Archimedes also ensures that their simulations will still be running when today's parallel hardware is obsolete. Indeed, earthquake engineering students in our lab have been writing Archimedes parallel programs and running them on the T3D without any concern for the underlying parallel hardware or system software. This insulation has not come at the price of performance; we regularly observe 30 megaflops per processor on the T3D, which is quite good for irregular sparse matrix calculations.
The second reason for creating Archimedes is that it eases the process of prototyping different numerical algorithms. With the basic library of primitives in place, we can quickly experiment with different time integration schemes, preconditioners, and element types. During the course of our research, we studied implicit versus explicit methods, lumped versus consistent mass matrices, first-order versus second-order absorbing boundaries, linear versus quadratic finite elements, and bubble-mode-enhanced versus standard Lagrange elements. The ability to express numerical algorithms in an intuitive, sequential manner was crucial in allowing us to study the implications of our numerical decisions, before we settled on our current choices. The functionality of the Archimedes language continues to grow in response to new algorithmic needs.
Our final motivation in designing Archimedes is that a number of the numerical and computational issues faced in modeling earthquake-induced ground motion are shared by many other applications in computational science and engineering. Unstructured mesh methods are useful for PDE problems that are characterized by complex geometries or that exhibit multiscale phenomena, such as transonic flows, crack propagation, large deformation materials processing, and pollutant transport, or . Our goal was to make Archimedes useful for this broader class of problems. Indeed, Archimedes is now being used in several areas other than ground motion modeling.
Many researchers do not wish to bother with low level details of programming a parallel machine, yet still want the efficiency associated with message-passing code. The Archimedes code generator is designed so that it can be extended by users without having to rebuild the system. For example, users can write their own parallel preconditioner routines and register them with the Archimedes compiler without recompiling any code. This provides a mechanism for the system to grow and evolve.