
Well, I stand up next to a mountain, I chop it down with the edge of my hand
Well, I pick up all the pieces and make an island, might even raise a little sand
-- Jimi Hendrix
|
Michael Erdmann

|
|
| 
| 
|
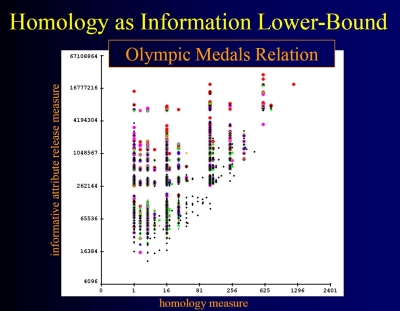
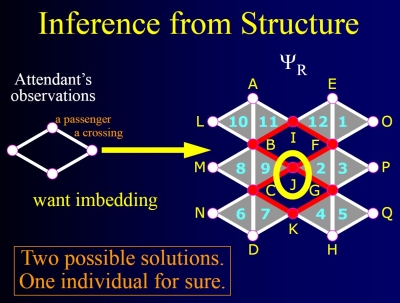
Information has intrinsic geometric and topological structure, arising from relative relationships beyond absolute values or types. For instance, the fact that two people did or did not share a meal describes a relationship independent of the meal's ingredients.
Multiple such relationships give rise to relations and their lattices. Lattices have topology. That topology informs the ways in which information may be observed, hidden, inferred, and dissembled. Privacy preservation may be understood as finding isotropic topologies, in which relations appear homogeneous. Moreover, the underlying lattice structure of those topologies has a temporal aspect, which reveals how isotropy may contract over time, thereby puncturing privacy.
Here is a report: Topology of Privacy: Lattice Structures and Information Bubbles for Inference and Obfuscation. Errata
An application: Deception, Delay, and Detection of Strategies.

In June 2003, a sizeable group of Topologists and Roboticists gathered at ETH in Zurich, Switzerland for a collaborative workshop. The goal of the workshop was to explore robotic motions using newly discovered topological perspectives and to build the foundations of a long-term research agenda. A brief writeup appeared in Science. Here are some pictures I took of the attendees.
In July 2006, a similar group of Topologists and Roboticists again gathered at ETH in Zurich. I did not take any pictures this time, but here is a list of the talks.
Between August 2006 and July 2012, my research was part of a multi-year multi-institutional effort involving topologists and roboticists working on a variety of problems at the interface of algebraic topology and autonomous systems. This research effort, called SToMP (Sensor Topology and Minimal Planning), was led by Robert Ghrist.
Two papers related to this work:

|
Line Weavings for the
Astral 40 set of representative proteins Structural Comparisons for a basis set of proteins | 
|
Proteins, Knots, and Line Weavings
Algorithms for comparing protein structures using geometric convolution and line weavings.
An early
version (without line weavings) of this report appeared at RECOMB 2004.
A
revised version (with line weavings and similarity trials)
appeared in the
Journal of Computational Biology.
(Clarification/Erratum: In Section 6.2.3 of the paper we defined the
"L2 measure" using a sum of integrals, each measuring a squared error
between two lines. Our code inadvertently computed the sum of
the square roots of these integrals. Thus the dimensions of the "L2"
values reported are actually square-root-Angstroms not Angstroms.)

 |
|
|