 is known. With a mixture of Gaussians, one
interpretation of this assumption is that we know
is known. With a mixture of Gaussians, one
interpretation of this assumption is that we know  and
and
 for each Gaussian. In that case, our application of
EM will estimate only
for each Gaussian. In that case, our application of
EM will estimate only 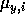 ,
, 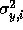 , and
, and
 .
.



In the context of active learning, we are assuming that the input
distribution  is known. With a mixture of Gaussians, one
interpretation of this assumption is that we know
is known. With a mixture of Gaussians, one
interpretation of this assumption is that we know  and
and
 for each Gaussian. In that case, our application of
EM will estimate only
for each Gaussian. In that case, our application of
EM will estimate only 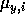 ,
, 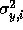 , and
, and
 .
.
Generally however, knowing the input distribution will not correspond
to knowing the actual  and
and  for each
Gaussian. We may simply know, for example, that
for each
Gaussian. We may simply know, for example, that 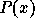 is uniform, or
can be approximated by some set of sampled inputs. In such cases, we
must use EM to estimate
is uniform, or
can be approximated by some set of sampled inputs. In such cases, we
must use EM to estimate  and
and  in addition
to the parameters involving y. If we simply estimate these values
from the training data, though, we will be estimating the joint
distribution of
in addition
to the parameters involving y. If we simply estimate these values
from the training data, though, we will be estimating the joint
distribution of  instead of
instead of 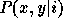 . To obtain a
proper estimate, we must correct Equation 5 as
follows:
. To obtain a
proper estimate, we must correct Equation 5 as
follows:
Here, 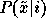 is computed by applying
Equation 7 given the mean and x variance of the
training data, and
is computed by applying
Equation 7 given the mean and x variance of the
training data, and  is computed by applying the same equation
using the mean and x variance of a set of reference data drawn
according to
is computed by applying the same equation
using the mean and x variance of a set of reference data drawn
according to  .
.
If our goal in active learning is to minimize variance, we should
select training examples 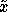 to minimize
to minimize
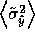 . With a mixture of
Gaussians, we can compute
. With a mixture of
Gaussians, we can compute  efficiently. The model's estimated distribution of
efficiently. The model's estimated distribution of  given
given
 is explicit:
is explicit:
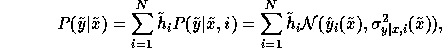
where 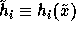 , and
, and  denotes the normal distribution with mean
denotes the normal distribution with mean  and variance
and variance
 . Given this, we can model the change in each
. Given this, we can model the change in each  separately, calculating its expected variance given a new point
sampled from
separately, calculating its expected variance given a new point
sampled from 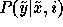 and weight this change by
and weight this change by
 . The new expectations combine to form the learner's new
expected variance
. The new expectations combine to form the learner's new
expected variance
where the expectation can be computed exactly in closed form:
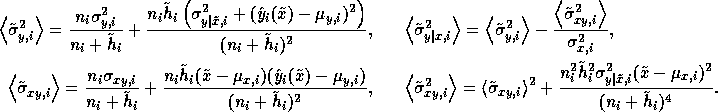
If, as discussed earlier, we are also estimating 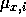 and
and
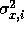 , we must take into account the effect of the new
example on those estimates, and must replace
, we must take into account the effect of the new
example on those estimates, and must replace  and
and
 in the above equations with
in the above equations with

We can use Equation 9 to guide active learning. By
evaluating the expected new variance over a reference set given
candidate  , we can select the
, we can select the  giving the lowest
expected model variance. Note that in high-dimensional spaces, it may
be necessary to evaluate an excessive number of candidate points to
get good coverage of the potential query space. In these cases, it is
more efficient to differentiate Equation 9 and hillclimb
on
giving the lowest
expected model variance. Note that in high-dimensional spaces, it may
be necessary to evaluate an excessive number of candidate points to
get good coverage of the potential query space. In these cases, it is
more efficient to differentiate Equation 9 and hillclimb
on  to find a locally maximal
to find a locally maximal  . See, for example,
[Cohn 1994].
. See, for example,
[Cohn 1994].


