

Next: Pseudo-Boolean constraints and extended
Up: Proof Complexity
Previous: Proof Complexity
To encode
a modularity constraint in this way, we first note that we can
easily capture an equality axiom of the form
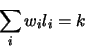 |
(34) |
in a pseudo-Boolean setting, simply by rewriting (34) as the pair of
constraints
In what follows, we will therefore feel free to write axioms of the
form (34).
We now denote by
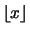 the floor of
the floor of  , which is to say
the smallest integer not greater than
, which is to say
the smallest integer not greater than  , and have:
, and have:
Proposition 3.19
Suppose that we have a modularity constraint
of the form (
33). We set
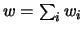
and introduce new
variables
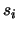
for
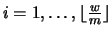
. Then (
33) is
equivalent to
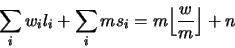 |
(35) |
Proof. Reducing both sides of (35) mod m shows that (35)
clearly implies (33). For the converse, note if (33) is
satisfied, there is some integer  such that
such that
 . Further, since
. Further, since
 , it follows
that
, it follows
that 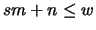 , so that
, so that
 and thus
and thus
 . We can therefore satisfy (35) by
valuing exactly that many of the
. We can therefore satisfy (35) by
valuing exactly that many of the 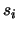 to be true.
to be true.

Understand that the introduction of new variables here is not part of
any intended inference procedure; it is simply the fashion in which
the modularity constraints can be captured within a pseudo-Boolean setting.
In the case where all of the constraints are parity constraints, we
have:
Proposition 3.20
A set of mod 2 constraints can be solved in
polynomial time.
Proof. An individual constraint (recall that 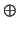 corresponds to
exclusive or, or addition mod 2)
corresponds to
exclusive or, or addition mod 2)
can be viewed simply as defining
and this definition can be inserted to remove  from the remaining
constraints. Continuing in this way, we either define all of the
variables (and can then return a solution) or derive
from the remaining
constraints. Continuing in this way, we either define all of the
variables (and can then return a solution) or derive 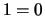 and can
return failure.
and can
return failure.

This result, which can be thought of as little more than an
application of Gaussian elimination, is also an instance of a far more
general result of Schaefer's Schaefer:complexity.
Proposition 3.21
A set of mod 2 constraints can be solved in
polynomial time using the pseudo-Boolean axiomatization given by
(
35).
Proof. The technique is unchanged. When we combine
and
we get
and can now treat  as one of the auxiliary
as one of the auxiliary  variables. Eventually,
we will get
variables. Eventually,
we will get
for a large (but polynomially sized) set 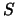 of auxiliary variables
and some
of auxiliary variables
and some 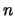 that is either even or odd. If
that is either even or odd. If 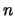 is even, we can value
the variables and return a solution; if
is even, we can value
the variables and return a solution; if 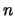 is odd and there are
is odd and there are 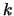 auxiliary variables, we have
auxiliary variables, we have
so
 |
(36) |
since each 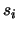 is integral. But we also have
is integral. But we also have
so that
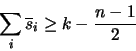 |
(37) |
Adding (36) and (37) produces 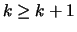 , a
contradiction.
, a
contradiction.

Let us point out, however, that if a mod 2 constraint is encoded in a
normal Boolean way, so that
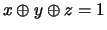 becomes
becomes
it is not obvious how the pseudo-Boolean analog can be reconstructed. Here is
the problem we mentioned at the beginning of this section: it is not
enough to simply extend the representation; we need to extend the
inference methods as well. In fact, even the question of whether
families of mod 2 constraints can be solved in polynomial time by pseudo-Boolean methods without the introduction of auxiliary variables as in
(35) is open. Other authors have also considered the problem
of reasoning with these constraints directly [LiLi2000].


Next: Pseudo-Boolean constraints and extended
Up: Proof Complexity
Previous: Proof Complexity
Matt Ginsberg
2004-02-19
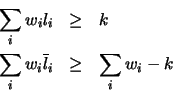
![]() the floor of
the floor of ![]() , which is to say
the smallest integer not greater than
, which is to say
the smallest integer not greater than ![]() , and have:
, and have:
![]() such that
such that
![]() . Further, since
. Further, since
![]() , it follows
that
, it follows
that ![]() , so that
, so that
![]() and thus
and thus
![]() . We can therefore satisfy (35) by
valuing exactly that many of the
. We can therefore satisfy (35) by
valuing exactly that many of the ![]() to be true.
to be true.
![]()
![]() corresponds to
exclusive or, or addition mod 2)
corresponds to
exclusive or, or addition mod 2)
![]() becomes
becomes