Butterfly and dilated butterfly networks belong to a larger class of
networks called splitter networks. The switches on each level
of a splitter network can be partitioned into blocks. All of the
switches on level 0 belong to the same block. On level 1, there
are two blocks, one consisting of the switches that are in the upper
rows, and the other consisting of the switches that are in the
lower 
rows. In general, the switches in a block B of size
on level l have neighbors in two blocks, 
and 
,
on level l+1, where u stands for upper and l for
lower. The upper block, 
, contains the switches on level l+1
that are in the same rows as the upper 
switches of B. The
lower block, 
, consists of the switches that are in the same rows
as the lower 
switches of B. The edges from B to 
are
called the up edges, and those from B to 
are called
the down edges. The three blocks, B, 
, and 
, and
the edges between them are collectively called a splitter. The
switches in B are called the splitter inputs, and those in
and 
are called the splitter outputs. In a splitter
network with multiplicity d, each splitter input has d
outgoing up edges and d outgoing down edges, and each splitter
output has 2d incoming edges. In a d-dilated butterfly, the d
up (and d down) edges out of each splitter input all lead to the
same splitter output, but this need not be the case in general. For
example, we have illustrated an 8-input splitter network with
multiplicity 2 in Figure 2.
Figure 2: An
8-input splitter network with multiplicity 2.
In a splitter network, each input and output are connected by a single logical (up-down) path through the blocks of the network. The path is determined by the address of the output. At the ith level of the network, an up edge is taken if the ith bit of the output's address is 0. Otherwise a down edge is taken. As an example, Figure 3 shows the logical path from any input to output 011, which consists of an up edge followed by two down edges. In a butterfly, this logical path specifies a unique path through the network, since only one up and one down edge emanate from each switch. (In fact, a splitter network with multiplicity one is very similar to a delta network [5].) In a general splitter network with multiplicity d, however, each switch will have d up and d down edges, and each step of the logical path can be taken on any one of d edges. Hence, one logical path can be realized by a myriad of physical paths in a general splitter network.
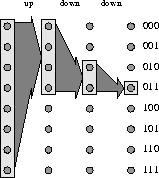
Figure 3: The logical path from any input
to output 011.