

Next: Linear Programming
Up: Bound Propagation
Previous: Introduction
What Bounds Can Learn From Each Other
Consider a Markov network defined by the potentials
 each dependent on a set of nodes
each dependent on a set of nodes  .
The probability to find the network in a certain state
.
The probability to find the network in a certain state  is
proportional to
is
proportional to
 |
(1) |
Problems arise when one is interested in the marginal probability over a
small number of nodes (denoted by
 ), since in general this
requires the summation over all of the exponentially many states.
), since in general this
requires the summation over all of the exponentially many states.
Figure:
Examples of separator and marginal nodes in an (infinite)
Ising grid. Light shaded nodes correspond to
 , black nodes
to
, black nodes
to
 . (a) A single node enclosed by its tightest separator.
(b), (c) Two marginal nodes enclosed by their tightest separator. (d)
Another choice for a separator for a single node marginal; the other
node enclosed by that separator belongs to
. (a) A single node enclosed by its tightest separator.
(b), (c) Two marginal nodes enclosed by their tightest separator. (d)
Another choice for a separator for a single node marginal; the other
node enclosed by that separator belongs to
 .
.
 |
Let us define the set of separator nodes,
 , to be the nodes
that separate
, to be the nodes
that separate
 from the rest of the network. One can take,
for instance, the union of the nodes in all potentials that contain at
least one marginal node, while excluding the marginal nodes itself in that
union (which is the Markov blanket of
from the rest of the network. One can take,
for instance, the union of the nodes in all potentials that contain at
least one marginal node, while excluding the marginal nodes itself in that
union (which is the Markov blanket of
 ):
):
 |
(2) |
See for instance Figure ![[*]](crossref.png) a-c. It is not necessary,
however, that
a-c. It is not necessary,
however, that
 defines a tight separation. There can
be a small number of other nodes,
defines a tight separation. There can
be a small number of other nodes,
 , inside the separated
area, but not included by
, inside the separated
area, but not included by
 (Figure
(Figure ![[*]](crossref.png) d).
A sufficient condition for the rest of the theory is that the size of
the total state space,
d).
A sufficient condition for the rest of the theory is that the size of
the total state space,
 ,
is small enough to do exact computations.
,
is small enough to do exact computations.
Suppose that we know a particular setting of the separator nodes,
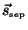 , then computing the conditional distribution of
, then computing the conditional distribution of
 given
given
 is easy:
is easy:
 |
(3) |
This expression is tractable to compute since
 serves as the
Markov blanket for the union of
serves as the
Markov blanket for the union of
 and
and
 . Thus the actual numbers
are independent of the rest of the network and can be found either by
explicitly doing the summation or by any other more sophisticated method.
Similarly, if we would know the exact distribution over the separator nodes,
we can easily compute the marginal probability of
. Thus the actual numbers
are independent of the rest of the network and can be found either by
explicitly doing the summation or by any other more sophisticated method.
Similarly, if we would know the exact distribution over the separator nodes,
we can easily compute the marginal probability of
 :
:
 |
(4) |
Unfortunately, in general we do not know the distribution
 and therefore we cannot compute
and therefore we cannot compute
 . We can, however,
still derive certain properties of the marginal distribution, namely
upper and lower bounds for each state of
. We can, however,
still derive certain properties of the marginal distribution, namely
upper and lower bounds for each state of
 . For instance,
an upper bound on
. For instance,
an upper bound on
 can easily be found by computing
can easily be found by computing
 |
(5) |
under the constraints
 and
and
 . The distribution
. The distribution
 corresponds to
corresponds to
 free parameters
(under the given constraints) used to compute the worst case (here:
the maximum) marginal value for each
free parameters
(under the given constraints) used to compute the worst case (here:
the maximum) marginal value for each
 . Obviously, if
. Obviously, if
 the upper bound corresponds to the
exact value, but in general
the upper bound corresponds to the
exact value, but in general
 is unknown and we have to
maximize over all possible distributions.
One may recognize Equation
is unknown and we have to
maximize over all possible distributions.
One may recognize Equation ![[*]](crossref.png) as a simple linear programming
(LP) problem with
as a simple linear programming
(LP) problem with
 variables. With a similar
equation we can find lower bounds
variables. With a similar
equation we can find lower bounds
 .
.
Upto now we did not include any information about
 we might have into the equation above. But suppose that we
already computed upper and lower bounds on the marginals of other
nodes than
we might have into the equation above. But suppose that we
already computed upper and lower bounds on the marginals of other
nodes than
 . How can we make use of this knowledge?
We investigate our table of all sets of marginal nodes we bounded
earlier and take out those that are subsets of
. How can we make use of this knowledge?
We investigate our table of all sets of marginal nodes we bounded
earlier and take out those that are subsets of
 . Obviously,
whenever we find already computed bounds on
. Obviously,
whenever we find already computed bounds on
 where
where
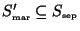 1,
we can be sure that
1,
we can be sure that
![\begin{displaymath}
\sum_{\vec s_\mathrm{\scriptscriptstyle sep}\in S_\mathrm{\s...
...makebox[0pt][l]{$ '$}}_\mathrm{\scriptscriptstyle mar}\right)
\end{displaymath}](img26.png) |
(6) |
and similarly for the lower bound. These equations are nothing more
than extra contraints on
 which we may include in the
LP-problem in Equation
which we may include in the
LP-problem in Equation ![[*]](crossref.png) .
There can be several
.
There can be several
 that are subsets of
that are subsets of
 each
defining
each
defining
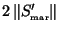 extra constraints.
extra constraints.
In this way, information collected by bounds computed earlier, can
propagate to
 , thereby finding tighter bounds for these
marginals. This process can be repeated for all sets of marginal
nodes we have selected until convergence is reached.
, thereby finding tighter bounds for these
marginals. This process can be repeated for all sets of marginal
nodes we have selected until convergence is reached.
Subsections


Next: Linear Programming
Up: Bound Propagation
Previous: Introduction
Martijn Leisink
2003-08-18
![]() each dependent on a set of nodes
each dependent on a set of nodes ![]() .
The probability to find the network in a certain state
.
The probability to find the network in a certain state ![]() is
proportional to
is
proportional to

![]() , to be the nodes
that separate
, to be the nodes
that separate
![]() from the rest of the network. One can take,
for instance, the union of the nodes in all potentials that contain at
least one marginal node, while excluding the marginal nodes itself in that
union (which is the Markov blanket of
from the rest of the network. One can take,
for instance, the union of the nodes in all potentials that contain at
least one marginal node, while excluding the marginal nodes itself in that
union (which is the Markov blanket of
![]() ):
):
![[*]](crossref.png) a-c. It is not necessary,
however, that
a-c. It is not necessary,
however, that
![[*]](crossref.png) d).
A sufficient condition for the rest of the theory is that the size of
the total state space,
d).
A sufficient condition for the rest of the theory is that the size of
the total state space,
![]() , then computing the conditional distribution of
, then computing the conditional distribution of
![]() given
given
![]() is easy:
is easy:
![]() and therefore we cannot compute
and therefore we cannot compute
![]() . We can, however,
still derive certain properties of the marginal distribution, namely
upper and lower bounds for each state of
. We can, however,
still derive certain properties of the marginal distribution, namely
upper and lower bounds for each state of
![]() . For instance,
an upper bound on
. For instance,
an upper bound on
![]() can easily be found by computing
can easily be found by computing
![[*]](crossref.png) as a simple linear programming
(LP) problem with
as a simple linear programming
(LP) problem with
![]() we might have into the equation above. But suppose that we
already computed upper and lower bounds on the marginals of other
nodes than
we might have into the equation above. But suppose that we
already computed upper and lower bounds on the marginals of other
nodes than
![]() . How can we make use of this knowledge?
We investigate our table of all sets of marginal nodes we bounded
earlier and take out those that are subsets of
. How can we make use of this knowledge?
We investigate our table of all sets of marginal nodes we bounded
earlier and take out those that are subsets of
![]() . Obviously,
whenever we find already computed bounds on
. Obviously,
whenever we find already computed bounds on
![]() where
where
![]() 1,
we can be sure that
1,
we can be sure that
![[*]](crossref.png) .
There can be several
.
There can be several
![]() , thereby finding tighter bounds for these
marginals. This process can be repeated for all sets of marginal
nodes we have selected until convergence is reached.
, thereby finding tighter bounds for these
marginals. This process can be repeated for all sets of marginal
nodes we have selected until convergence is reached.