
Next: Diverging Counter
Up: Invariants
Previous: OddCounter
This example has two purposes.
One is
to give another example of an invariant. The other is
to hint at how state machines are appropriate models of abstract
data types, as you might implement in your favorite object-oriented language.
Here is a description of a FatSet abstract data
type modeled as a state machine:
-
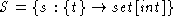 .
The state variable, t, maps to a set of integers.
.
The state variable, t, maps to a set of integers. -
 .
The set of initial states is the set of states that
map t to a singleton set. Notice that there are an infinite number
of initial states.
.
The set of initial states is the set of states that
map t to a singleton set. Notice that there are an infinite number
of initial states. - A =
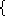 union(u: set[int])/ok(), card()/ok(int)
union(u: set[int])/ok(), card()/ok(int) 
-
 =
=
1
unionĒ(u: set[int])/ok()
pre 
post 
card()/ok(int)
pre true
post 
Suppose I want to show the property that the size of the
FatSet t is always greater than or equal to 1:
Here's an informal proof:
- It's true of all initial states since the size of all singleton sets
is 1.
- We need to show the invariant is preserved for each of
union
and card.
- (union). Assume
- u is nonempty (i.e., the pre-condition holds in the pre-state),
- t's size is
 (i.e., the invariant holds in the pre-state), and
(i.e., the invariant holds in the pre-state), and -
 (i.e., the post-condition holds in the pre- and post-states)
(i.e., the post-condition holds in the pre- and post-states)
Then I need to show that the size of t' is  . This is true since
taking the union of two non-empty sets (t and u) is a non-empty
set,
whose size is
. This is true since
taking the union of two non-empty sets (t and u) is a non-empty
set,
whose size is  .
. - (card). Assume
- t's size is
 (i.e., the invariant holds in the pre-state), and
(i.e., the invariant holds in the pre-state), and -
 (i.e., the post-condition holds in the pre- and post-states)
(i.e., the post-condition holds in the pre- and post-states)
Then I need to show that the size of t' is  . This is true since
t' = t and t's size is
. This is true since
t' = t and t's size is  .
.
Notice how awful it would be if I had to write out these proof steps
in gory detail!
Two points about this example:
- You should notice that
the only interesting part of the proof above was for union,
the only action that changes the value of any state variable.
An action that changes the state of some state variable is called
a mutator.
I didn't really have anything to prove for card because
the action does not change the state of any state variable. I'll call
such an action a non-mutator.
In practice, we need to show only for mutators that the invariant
is preserved because non-mutators by definition
cannot change state. So if the invariant holds before the non-mutator
is called (pre-state); then it holds afterwards (post-state).
- Second I deliberately chose a value space for t that
includes ``unreachable values.'' In particular, t can never
be the empty set because it starts out non-empty and always remains
non-empty. But, remember, I need to show the invariant
holds of only reachable states.
Now, suppose I added a delete action to my FatSet example.
Let delete have the following behavior:
1
deleteĒ(i:int)/ok()
pre 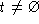
post 
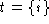 (where i is the argument to delete)
then the size of t' would be 0.
(where i is the argument to delete)
then the size of t' would be 0.


Next: Diverging Counter
Up: Invariants
Previous: OddCounter
Norman Papernick
Mon Mar 18 14:28:12 EST 1996






![]()