OddCounter

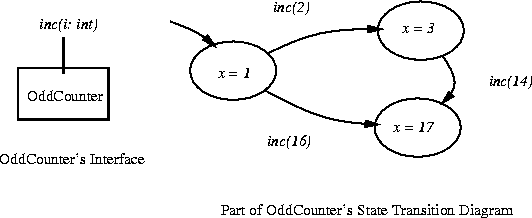
Let OddCounter be the state machine:

More precisely,

OddCounter = (



=

1

 incĒ(i: int)

             		pre i is even

             		post x' = x + i 

).

The invariant I want to prove is that OddCounter's state always holds an odd integer:

x is odd.

Intuitively we see this is true because

1. It's true of the initial state (1 is an odd integer).
2. For the action inc:
   • I assume:
     • i is even (i.e., the pre-condition holds in the pre-state),
     • x is odd (i.e., the invariant holds in the pre-state), and
     • x' = x + i (i.e., the post-condition holds in the pre- and post-states)
   • I need to show that x' is odd.
     • This is true since from facts about numbers I know an odd number (x) plus an even number (i) is always odd.