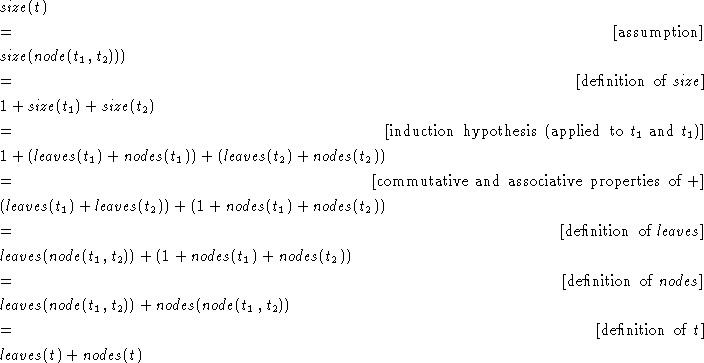Based on what we've said about our definitions, there is a pretty obvious connection between the three definitions give above. That is, we would expect the size of a tree to be the sum of the leaves and the nodes. We can make this precise as follows:
![]()
We will prove this by structural induction. As with natural deduction there are two cases: a base case for leaves, and an induction case for composite trees. Here is how it goes:
Proof:
Let t: TREE.
Base Case: Assume t is a leaf.

Induction Case: Assume that ![]() and that the
theorem hold for all trees t':TREE such that size(t') < size(t).
and that the
theorem hold for all trees t':TREE such that size(t') < size(t).