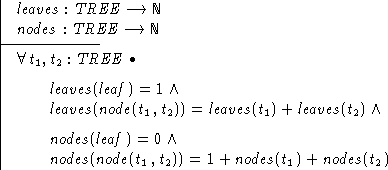There are also many ways that we might define the size of a tree. Some definitions would count just the leaves, others just the nodes. Here we will count both.
Informally, we could say that the size of a single leaf is 1, while
the size of a tree built out of two subtrees, say 
and 
, is
the sum of the sizes of the two subtrees plus 1 (for the joining node).
The basic idea of this definition is that we define the size of a tree
inductively over the structure, saying how the size of a given tree is
calculated from sizes its parts. Putting this more formally in the notation of
Software Engineering Mathematics, we would define a function by
first declaring its type (in this case 
), and
then saying how it is defined in each of the two cases.
[Note: I am doing things a little differently than what I tried to do in class. Here I am simply asserting that this is the definition of size; in class I tried to prove something about this definition.]
In a similar way, we might make other definitions about trees. Here are two useful ones:
