Figure 3: Variables in the Estimation Problem
Pose estimation has received attention in several domains, related to marine, terrestrial, aeronautic, and space navigation. There are two essentially different ways to obtain pose: integrating measurements that are internal to the moving equipment (dead reckoning), and relying on measurements that are external to the moving equipment. Dead reckoning is only accurate to a point; errors accumulate and performance degrades. External measurements of pose are necessary for absolute pose estimation. A mobile robot performing a long traverse on the Moon (or other celestial bodies) poses a great challenge for pose estimation technologies. The GPS infrastructure is not available, and the magnetic field is insufficient for compass measurements. On celestial bodies, attitude measurements can be generated accurately from a star sensor [16], since the visibility of stars from bodies without atmosphere is excellent. In this situation, relative position and absolute orientation are available, but absolute position is not.
Our solution is to use landmarks detected visually in the environment to fix position, as usually done in marine navigation. But instead of relying on human expertise, we free the operator from this burden by relying on vision techniques for detection of landmarks and position estimation.
Other researchers have studied the possibility of vision-based localization in outdoor applications [4, 7, 11, 13, 14], but real data analysis has been scarce (the only data available data sets have been produced by Thompson and his group [14]).
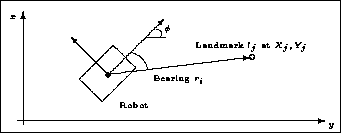
With visual observations, each image feature can be converted to an angle in the robot's coordinate system; the angle is called a bearing (Figure 3). The image contains a set of image bearings. The map contains a number of landmarks . The pose of the robot in the global coordinate system is ( is orientation). An interpretation of the image is a set of correspondences between image features and map features.

Figure 3: Variables in the Estimation Problem