
Fabio Cozman Eric Krotkov
Robotics Institute, Carnegie Mellon University, Pittsburgh
{ fgcozman, epk } @cs.cmu.edu
http://www.cs.cmu.edu/~{ fgcozman, epk }
Light power is affected when it crosses the atmosphere; there is a simple, albeit non-linear, relationship between the radiance of an image at any given wavelength and the distance between object and viewer. This phenomenon is called atmospheric scattering and has been extensively studied by physicists and meterologists. We present the first analysis of this phenomenon from an image understanding perspective: we investigate a group of techniques for extraction of depth cues solely from the analysis of atmospheric scattering effects in images. Depth from scattering techniques are discussed for indoor and outdoor environments, and experimental tests with real images are presented. We have found that depth cues in outdoor scenes can be recovered with surpr is in g accuracy and can be used as an additional information source for autonomous vehicles.
Observers of outdoor scenery witness a variety of atmospheric effects caused by light scattering: the sky is blue, distant mountains appear bluer than nearby mountains, a flashlight beam is reflected back by a foggy environment. Such phenomena have been actively studied by physicists, meterologists and navigators [7, 8]. In this paper, we present the first analysis of atmospheric scattering from an image understanding perspective. We investigate techniques that extract depth cues from atmospheric scattering effects in images. We use the phrase depth from scattering to refer to such techniques.
Investigators have studied atmospheric scattering with distinct goals. Physicists and navigators seek to predict how a particular atmosphere affects visual perception; computer graphics researchers simulate scattering rather than measure its effect in practice [4, 6]. Artists have used simulated atmospheric effects in paintings at least since the Renaissance [1]. Our purpose is new: we use atmospheric scattering as a beneficial source of information about geometric relationships among objects and a viewer.
Light power and intensity are modified principally by scattering when light crosses the atmosphere. The presence of small particles suspended in the atmosphere causes the light to scatter in a variety of directions. Given a number of assumptions discussed in the paper, we derive a relationship between the radiance of an image at any given wavelength and the distance between object and viewer. Section 2 is devoted to the derivation of this model.
The inter-dependence of scattering and distance opens the possibility of recovering depth cues from images. We investigate the application of depth from scattering techniques in indoor and outdoor environments, discussing the extent to which the assumptions indicated in the modeling stage are fulfilled (section 3). We have found that depth cues in outdoor scenes can be recovered with with surpr is in g accuracy. Our experiments and results are described in sections 4 and 5.
Light scattering occurs when light interacts with particles suspended in the atmosphere. Effects of scattering are felt daily as we perceive the sky to be blue or reddish, depending on atmospheric conditions and solar illumination. The first successful model of scattering was developed by Lord Rayleigh in 1871, after a long period where researchers postulated that the sky was blue due to the presence of water in the atmosphere [7].
If particles in the atmosphere are spherical or small, light is scattered symmetrically with respect to incident rays of light [4]. We represent the portion of light that is scattered by a function B(lambda,theta), the angular scattering function. The variable theta is the angle between the incident ray of light and the emanating ray of light; lambda is the wavelength.

Atmospheric scattering manifests itself through two phenomena, which we discuss separately. The first phenomenon is attenuation of power; the second phenomenon is sky intensity.
Take a beam of light projected through a scattering medium, as
illustrated in Figure 1. The distance
between object and viewer is d. As rays of light are deflected by
particles, the power of light conveyed by
the beam decreases. For a differential portion of the trajectory,
power decreases as dP = - betaP dd [7],
where Po(lambda) is the power of the source and beta(lambda)
is called the extinction coefficient![]() .
By integration through the whole path,
the received power intensity is given by:
.
By integration through the whole path,
the received power intensity is given by:
P(lambda) = Po(lambda)
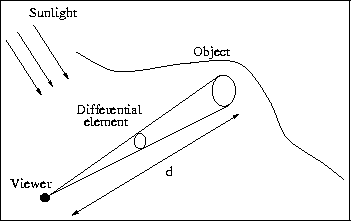
Figure 1: Light travels from an object to a viewer through the atmosphere
under uniform illumination (sunlight)
We are interested in the intensity of an image taken by the viewer. Two factors affect the relationship between power and intensity. Power decreases with distance by the inverse square law so power decreases with d2; on the other hand, intensity at a receiver increases with square of distance d2, because the solid angle subtended by the receiver corresponds to a larger area on the object [3]. Appendix A shows how the two effects cancel each other, so that the dependency of distance remains restricted to the exponential term.
For an object with intensity Io(lambda) in the absence of scattering and distance d from the viewer, the intensity measured by the viewer I(lambda) is:
I(lambda) = Io(lambda)
Even though light power is attenuated by direct scattering, there is another effect, also due to scattering, which increases the power in a light beam. We now model this phenomenon using some additional assumptions.
Consider an imaginary line, traced from the viewer to some point infinitely far away in a scattering medium. Suppose the line is illuminated by a uniform source from the top (for example, the sky). At each point of the line, scattering events take place and divert light from its original path.
As light is directed to the viewer from all points in the line, the viewer perceives a new source of light, due exclusively to scattering.
From the previous sections, we know that the light coming from any point at distance x is affected by the angular scattering function and is attenuated exponentially. To obtain the amount of light received in this manner, we integrate the effect of scattering events from the viewer to an arbitrary distance d:
I(lambda) = int0d Io(lambda) B(lambda, theta)
I(lambda) = { Io(lambda) B(lambda, theta) }/{ beta(lambda) }
(1 -
The integration assumes:
![]()
The first assumption is reasonable for the sky, and can possibly be approximated in large indoor environments. The second assumption is an approximation based on empirical observations [8].
In order to reduce the complexity of the scattering model above, we make the following assumption:
Under this assumption, call sky intensity S(lambda) the quantity { Io(lambda) B(lambda) }/{ beta(lambda) } . If a viewer were to look at a point infinitely far away (d rarrinf), the perceived intensity would be S(lambda), solely caused by atmospheric scattering.
The two effects above, attenuation and sky intensity, are additive due to the linear character of light propagation [8]. Suppose an object located at distance d has intensity Io(lambda) when imaged in a vacuum. In the presence of atmosphere the intensity is:
I(lambda) =
So far we have kept the dependencies on wavelength lambda explicit.
In a non-polluted atmosphere, without rain or snow,
scattering is mainly caused by small particles and is
sensitive to the wavelength![]() .
Variations across wavelength are small, and can only be perceived
distinctly for large distances. For the distances involved in our
experiments (between 1000 to 3000 meters), there is no appreciable ``blueing''
effect. For larger particles, wavelength selectivity decreases remarkably.
For dense concentrations of clean water droplets such that visibility
falls below 1000 meters (a situation defined as fog [8]),
the dependence on wavelength becomes negligible. Due to such considerations,
we drop the dependency on lambda in the remainder of this paper,
since it has no effect relevant to our experiments.
We refer to the measured intensity of
an object as C, and the intensity of the object without
scattering as C. We arrive at our basic equation:
.
Variations across wavelength are small, and can only be perceived
distinctly for large distances. For the distances involved in our
experiments (between 1000 to 3000 meters), there is no appreciable ``blueing''
effect. For larger particles, wavelength selectivity decreases remarkably.
For dense concentrations of clean water droplets such that visibility
falls below 1000 meters (a situation defined as fog [8]),
the dependence on wavelength becomes negligible. Due to such considerations,
we drop the dependency on lambda in the remainder of this paper,
since it has no effect relevant to our experiments.
We refer to the measured intensity of
an object as C, and the intensity of the object without
scattering as C. We arrive at our basic equation:
C = C
Equation (3) relates a number of physical quantities to the quantity of interest, the distance between viewer and object d. We can obtain information about depth by exploring these relationships.
Take an object immersed in non-vacuous atmosphere. Suppose we take a picture of this object through a color filter, and segment the intensities so that we can obtain average intensities for regions of approximately identical intensities. For each region, this gives us C in equation (3). In order to obtain d, we also need C, the intensity of the object without atmospheric attenuation; beta, the extinction coefficient, and S, the sky intensity. We must find ways to handle the four unknowns d, C, beta and S in this equation, by measuring some of them separately or by increasing the number of measurements.
We will assume that a single object yields a single equation (3), but in practice we can have several patches of homogeneous intensity in a single object. If two patches are virtually identical, then the two derived equations will be virtually identical and we gain nothing: in this case we should combine the patches and obtain a more reliable intensity average.
The sky intensity S can be measured from any image that contains a portion of the sky. In outdoor images, S is determined by averaging areas of the sky that are far from the Sun. In a laboratory experiment it is possible to obtain S if the atmosphere is densely filled with water vapor, so that distant objects cannot be seen at all (the ``sky'' intensity is the intensity of an area in which objects are indistinguishable).
If we can measure the illumination of an object with and without scattering effects, we have C and C respectively. We still would need the extinction coefficient beta in order to obtain d. Expression (3) yields:
If we have several objects, measurement of Ci, Ci and S allows us to obtain relative distances among objects. For each pair of objects:
{ di }/{ dj } = {
If we know the depth do for an object of known intensity Co, we can use the object as a ``fixed'' point. Using expression (5):
di = Ko
So far we have assumed the possibility of measuring the intensities of objects in the absence of scattering. This is a reasonable assumption when we can make close measurements in clean air. For example, a robot operating in a plant filled with dust, but aware of the form and color of the objects that exist in the plant, or an autonomous vehicle driving in a foggy road, trying to obtain depth cues for the road signs.
For general outdoor environments, objects are distant and produce small disparity; focusing alone cannot distinguish objects that are farther than a certain distance. On the contrary, light scattering is a depth cue that benefits from distance: the farther the object, the larger the effect of scattering.
The problem with outdoor environments is that we cannot measure their intensity without the atmosphere. In order to proceed, we will assume that uniform light reaches all areas of the scene and that vegetation and soil characteristics are homogeneous. Under this assumption, we expect all features to have approximately the same intensity were they imaged without scattering.
In this case we can still find useful three-place relations between objects. Consider three objects at distances di, dj and dk and measured intensities Ci, Ck and Ci respectively. We solve for the ratio of distance differences:
{ di - dk }/{ dj - dk } =
{
We tested expression (6) by taking a series of outdoor images in the area of Pittsburgh, Pennsylvania. Images were taken from a tripod containing a color camera over a rotary platform, a compass, a dual-axis inclinometer and a GPS system [2]. A panorama is formed by merging the images by the Kuglin/Hines method [5, 9]. The top of Figure 2 shows a mosaic made from a sequence of images taken by the river Allegheny.The mountains in the scene are numbered from 1 to 5; we refer to them as mi, i is in {1 ...5}. Topographic maps were obtained from the United States Geographic Survey (USGS).
Figure 2: Mosaic with images taken near the Allegheny river
The images in Figure 2 were obtained at latitude 40.474350E, longitude 79.965698N. Call di the distance from this point to the peak of the mountain mi; the ground truth values are given in Table 1.
| mi | di (m) | mi | di (m) |
| m1 | 827 | m2 | 1635 |
| m3 | 2151 | m4 | 876 |
| m5 | 1653 |
For each mountain in the panorama, we are interested in the average intensity across the image of the mountain. We then use these averages as the C values for the mountains in equation (6). The horizon is detected automatically through a search for high gradient pixels; these pixels are assumed to be horizon pixels. The bottom of Figure 2 shows the result of horizon detection. The local maxima of the horizon are then searched, and sequences of pixels are automatically grouped into mountain structures. The average intensity between the horizon and the bottom of the mountains is then calculated (in Figure 2, the average goes from the black horizon line down to the white horizontal line). The average intensities are used in the calculations discussed below.
We studied the accuracy of rijk, the dk ratio of di to dj. The calculation of rijk ratios depends on the choice of a mountain mk which appears in the numerator and denominator; call it the pivot. The choice of the pivot is crucial: if the pivot and another mountain are at the same distance from the viewer, the ratio will be grossly miscalculated. For example, we cannot calculate the d1 ratio of d2 to d4, because d1 and d4 are identical for practical purposes. We say two detected mountains ``conflict'' when their average intensities are approximately the same. A simple algorithm for the choice of a pivot, which uses the information about the horizon obtained above, is:
The average error in the first table is 9.1%; in the second table, 9.0%, in the third table, 10.5%. Overall, the average error is 9.4%.
We have observed that the effects of scattering vary greatly with atmospheric conditions and the position of the Sun. When sunlight is directly incident on the imaged mountains, scattering effects tend to be buried by the extreme brightness of the Sun. Scattering ratios are most effective when the Sun is behind the imaged mountains. The perception and understanding of scattering requires some prior notion of the atmospheric properties of the scenes being imaged; scattering is an additional, powerful depth cue available at little cost for the viewer.
|
2cmRatio pivot m3 | Ground Truth | Measured | Error |
| r123 | 0.3900 | 0.3350 | 14.1 % |
| r143 | 0.9628 | 1.0800 | 12.2 % |
| r153 | 0.3762 | 0.4044 | 7.5 % |
| r243 | 0.4051 | 0.3101 | 2.3 % |
| r253 | 0.9647 | 0.8285 | 14.1 % |
| r453 | 0.3908 | 0.3743 | 4.2 % |
|
2cmRatio pivot m1 | Ground Truth | Measured | Error |
| r231 | 0.6099 | 0.6649 | 9.0 % |
| r251 | 0.9779 | 1.1100 | 13.5 % |
| r351 | 0.6237 | 0.5955 | 4.5 % |
|
2cmRatio pivot m4 | Ground Truth | Measured | Error |
| r234 | 0.5948 | 0.6898 | 15.9 % |
| r254 | 0.9765 | 1.1020 | 12.9 % |
| r354 | 0.6091 | 0.6256 | 2.7 % |
Given the prom is in g results of outdoor experiments, the question arises: how well are the assumptions approximated in a small, closed indoor environment?
We studied a small environment to investigate the extent to which our assumptions were valid; we briefly describe our experiment, suggesting some aspects of our work that must receive further testing. We build a rectangular box of size 1.20 0.60 0.25 meter, with an entry for water vapor and two internal fans for distribution of vapor. Small rectangular, brightly colored objects, were placed in the box and imaged. Figure 3 graphs distance versus average intensity for measurements taken without vapor. The intensity gradually increases as the block receives light from a larger portion of the lamps, reaches a small area of uniform illumination and then decreases. The behavior of such illumination pattern is quite complex, as small changes in the position of the lights caused drastic changes in the intensity values. Such deviations caused errors up to plusmn20 cm, sometimes even resulting in the wrong order for the blocks. These results indicate that assumption 2 (uniformity of top illumination) cannot be properly enforced in such a small environment.
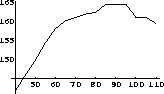
Figure 3: Variations in top illumination with distance
The paper contains an analysis of the physical properties of atmospheric scattering from an image understanding perspective. We presented a physical model for scattering and derived a set of techniques for recovery of depth cues based on scattering measurements. The 10 percent accuracy obtained in outdoor experiments is prom is in g; given the scarcity of depth cues in outdoor environments, such values indicate the possibility of using scattering when performing localization and outdoor image understanding. This is particularly relevant for space applications, in environments with atmosphere but without GPS or similar infrastructure. Experiments with indoor environments of larger dimensions are necessary to study the limits of our assumptions.
Physics based study of atmospheric interactions is an open area for research on the visual perception and understanding of our world; so far the computer vision community has concentrated most of the physical modeling to indoor, clean laboratory settings. Our work opens a number of possible questions for future exploration. For example, one could ask which depth cues can be extracted when single point sources of light are present in the environment. Understanding of outdoor scenery presents great challenges for autonomous, fully situated robots, which must grasp the variations of natural environments in order to interact with them.
Here we sketch the relation between light power and intensity, as they are affected by scattering attenuation. To simplify notation we drop the dependence on wavelength.
Consider an object at distance d from a lens and an image formed at distance -f from the lens. Suppose the lens has diameter l. If we pick a patch deltaO (with area A(deltaO)) in the object, this patch is imaged into a patch deltaM (with area A(deltaM)) in the image. Consider the line from the center of deltaM to deltaO; call alpha the angle between this line and the optical axis of the lens and theta the angle between the line and the normal at deltaO (a similar construction is used by Horn to derive radiometric properties of lenses [3]).
First, since the solid angles of deltaO and deltaM must be equal as
seen from the lens, we have the equality
{ A(deltaO) }/{ A(deltaM) } =
{
We are interested in the irradiance, which is measured by the camera sensor and produces the intensity values. Since the irradiance I is deltaP/A(deltaM), we obtain:
I = {(
 © Fabio Cozman[Send Mail?]
© Fabio Cozman[Send Mail?] Tue May 27 21:00:47 EDT 1997