Parsimonious Pirates

Thirteen pirates go on an extended voyage, pillaging and plundering from Africa to Asia. By the end they have quite a stash--too much to take back with them. They decide to lock it in a chest, leave the chest on an island, and come back for it a year later. Of course, not being terribly trusting, they want to ensure that none of them can come back early and claim the treasure for himself. They could just put 13 locks on it and each take a key, but a pirate's life is dangerous--they may not all be around in a year. What they want is for any majority of the original thirteen to be able to open the chest, while any fewer will be locked out. How many locks will it take for them to achieve this? The locks they are using are quite simple. Each key opens only one lock (no master keys), but keys can be duplicated, so multiple pirates can have keys to the same lock.

Prepared Prisoners

There are 100 prisoners in solitary confinement in a jail. The head guard decides to play a game with them. He will, at random intervals, randomly select one of them and take him out of his cell to a room with two lightbulbs. The prisoner can then choose to toggle the state of the lightbulbs (or he can do nothing). Before returning to his cell, he may choose to declare that all prisoners have been to the room. If he is correct, all the prisoners will be freed. If he is wrong, they will be executed. The prisoners cannot see the lightbulbs from their cells and they do not know the state of the lightbulbs at the start of the game. But they are allowed one evening together to decide on a strategy. What strategy should they follow to ensure that they all get released?

Directed Graphs

Prove that if each node in a directed graph has indegree > 0, then the graph must contain a cycle.

Restricted Rectangles

You have a rectangle, which is composed of smaller rectangles. Each of the interior rectangles has the property that at least one of its sides has an integer length. Prove that the larger rectangle has the same property.

Commensurate Cake

You are given a (two-dimensional) rectangular cake. Someone takes a rectangular piece from this cake. The piece can have any dimensions and orientation as long as it is rectangular. Your job is to cut the remaining cake into two pieces of equal area. You are only allowed to make one cut. And all you have to help you decide where to cut is a straightedge.

Hinged Mirrors

Consider two infinite planar mirrors as shown below. Prove that regardless of the angle between the mirrors, any beam of light that is directed at the mirrors bounces off of them only a finite number of times. That is, eventually the ray of light is such that it never again intersects a mirror. The ray of light is assumed to come from a "perfect laser", so it is infinitely thin. Also, the ray is never directed straight at the vertex, as the reflection from that point is undefined.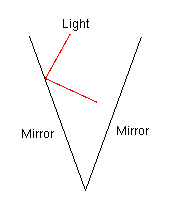

Coloring the Plane

Let each point in the Euclidian plane be colored either red or blue. Prove that there are two points of the same color which are unit distance apart.

Coloring the Plane (arbitrary distances)

Show that for any 2-coloring of the plane (as per the previous problem), there is a color for which you can find two same-colored points distance d apart for ALL distances d.

Coloring the Plane (3 colors)

Show that for any 3-coloring of the plane you can find two points of the same color which are unit distance apart. (Same as the first coloring problem, but with 3 colors).

Covering a Rectangle

Given a covering of a rectangle using n circles of radius r, prove that the same rectangle can be covered using 4n circles of radius r/2.

Sum and Product

Two integers, m and n, each between 2 and 100 inclusive, have been chosen. The product, mn, is given to mathematician P. The sum, m + n, is given to mathematician S. Their conversation is as follows:

What were the numbers?

Lightswitches

There is a line of 100 lightswitches, all initially off. If you toggle every lightswitch, then toggle every other lightswitch, then every third lightswitch, and so on until the only switch you flip is the last one, which switches will be on?

Probability Conversion

Given a biased coin which lands heads with probability 1/e, construct an experiment which, should it terminate, succeeds with probability 1/pi. The experiment can take an unbounded amount of time.