Nicholas Roy and Sebastian Thrun
Human beings take for granted their ability to move around and interact with each other in a wide range of environments. These same environments are tremendous sources of uncertainty for mobile robots. Not only does navigation introduce positional uncertainty, but systems that try to interact with human beings are faced with the tremendously noisy and ambiguous behaviours that humans exhibit.
The real problem is that it is often difficult to determine accurately what state the world is in. After a system takes an action in the world, it must almost always sense, to discover the outcome of that action. However, sensing is an imperfect operation; sensors do not always do a good job of identifying that outcome. Many planners can easily model the cost of sensing, but very few planners model how useful sensing can be.
The Partially Observable Markov Decision Process (POMDP) is a way to model uncertainty in a real world system's actions and perceptions [7]. Instead of making decisions based on the current perceived state of the world, the POMDP maintains a belief, or probability distribution, over the possible states of the world, and makes decisions based on the current belief. POMDPs are unfortunately useless for most real world problems due to the overwhelming computational complexity involved with planning in belief spaces.
However, the uncertainty that many real world problems exhibit often has a regular structure that can be exploited. By making assumptions about the kinds of beliefs that a system may have, it may be possible to reduce the complexity of finding policies that approximate the optimal POMDP policy, without being subject to the pain of finding the exact optimal policy. Being able to approximate optimal policies will allow for more reliable control in a number of situations, from motor control to system diagnosis. In particular, we focus on mobile robot motion planning and speech dialogue management.
Planning with uncertainty is not a new idea. However, the current state of the art suggests that modelling the world probabilistically leads to the most robust policies. POMDPs are the most general form of probabilistic planners, but finding policies for POMDP models is known to be computationally intractable. Exact solutions for POMDP policies are exponential in the size of the state-space, and the general finite-horizon stochastic POMDP is P-SPACE hard [3]. In general, exact solutions cannot be found for POMDPs of more than a handful of states.
Considerable work has been done in using approximate POMDP-style approaches for mobile robot control [4,5,1]. However, in all real-world applications of POMDP controllers, the policy is found using some heuristic approximation, such as voting or a dual-mode controller.
Some work has begun in modelling spoken dialogues using probabilistic planners and MDP models [2,6]. However, the MDP models are still somewhat limited, and we have shown that a POMDP-style planner can improve dialogue management performance in the face of degrading speech recognition.
Many problem domains have specific kinds of beliefs; furthermore, the kind of
beliefs that are likely in such domains can be represented compactly, or
summarised, by a sufficient statistic. We approximate the belief state of the
system using the joint statistics of the maximum-likelihood state and entropy
of the distribution
![]() over the states
over the states ![]() :
:
 |
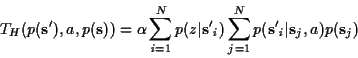 |
(1) |
[Museum
Map]
![\fbox{\includegraphics[height=1.25in]{figures/map-nmah.ps}}](img6.gif) [Conventional trajectory]
[Conventional trajectory]
![\fbox{\includegraphics[height=1.25in]{figures/conv3.ps}}](img7.gif) [POMDP trajectory]
[POMDP trajectory]
![\fbox{\includegraphics[height=1.25in]{figures/coastal3.ps}}](img8.gif)
|
The effect of using the higher-dimensional state space representation is that the expected reward becomes a function of the uncertainty of the belief state. For example, in the case of mobile robot navigation, a highly uncertain diffuse belief state will have lower expected reward for achieving the goal, and consequently the planner will prefer trajectories that trade off the cost of taking longer trajectories for the additional reward of having more positional certainty.
Figure 1 shows an example map on the left of the Smithsonian Museum of American History, and two example trajectories through the middle of the museum. The conventional trajectory takes the robot through the center of the open space where the laser sensors are likely to be blocked by people, and have less environmental structure to use for position tracking. The Augmented MDP trajectory takes the robot along the walls at the edges of the open space, away from the higher density of people, and closer to the environmental structure that helps localisation. This trajectory allows the robot attain its goal with higher certainty and reliability.
We have implemented the Augmented MDP also for spoken dialogue management aboard the nursebot, Florence Nightingale. We invert the traditional notion of state for spoken dialogues, considering the system state to be the intentions of the user, and consequently only partially observable through the utterances from the speech recognition system. In the face of reliable recognition, an MDP solution performs well, but as recognition begins to degrade, the necessity for information gathering and confirming actions are required that cannot be modelled by a conventional MDP.
By using the Augmented MDP as an approximator to a POMDP solution, we are able to show that the average reward per action changes for two different users with different recognition rates. For a user with low recognition rates, the average reward per action is 36.95 for the POMDP, but only 6.19 for the conventional MDP, suggesting the MDP responds incorrectly fairly often. For a user with higher recognition rates, the two systems were roughly equivalent at 49.72 and 44.95 reward/action rates respectively.
Throughout the results presented here, the belief space was parameterised by the conjunction of the maximum-likelihood state and the entropy of the belief state. This may have been a reasonable representation for the mobile robot problem, however it is not likely that this generalises to all robot environments. This representation is also unsupported for the speech domain. The results for the speech domain suggest that the entropy alone provides some information guiding the policy but is likely to be quite sub-optimal.
The sensor model for the laser range sensor used by the mobile robot navigation problem is completely static. However, the speech model used by the dialogue management is not static; the emission probabilities used during planning are average estimates. Consequently, the AMDP policy may be optimal over several dialogues, but not for a single dialogue. One approach may be to replan every dialogue after each utterance, or update the emission probabilities to a new average value and replan.
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -debug -white -no_fork -no_navigation -address -split 0 -dir html -external_file nickr nickr.tex.
The translation was initiated by Daniel Nikovski on 2000-04-28