Learning the Causal Structure of Hybrid Belief Networks

Probabilistic or Bayesian or Belief networks (BNs) are compact and semantically clean representations of probabilistic independencies and possible dependencies among sets of variables. They are usually used to statistically characterize future data. However, their structure, when constructed from independence statements that are known to be true to a reasonable degree, can also provide insights to the application domain. BNs that are constructed in such a way are causal. The problem addressed here is that of constructing learning the causal structure of BNs from data in domains that may contain continuous as well as discrete variables. The problem of structure induction in discrete domains has received a lot of attention and is considered comparatively much easier.

Impact:

Modeling for the purpose of understanding the application domain (as opposed to merely probabilistically describing the domain interrelations) will benefit tremendously from the solution of structure induction in arbitrary domains. Important applications arise in medicine (drug, disease and patient data relationships), agriculture (crop yields, pesticide, fertilizer and environmental data interactions), marketing (customer habits, social and financial status and purchase patterns), and the physical sciences (physical law discovery), among many others.

State of the Art:

There is no mature approach that addresses the recovery of the domain structure as a BN in a causal manner in its full generality. There exist two special approaches to the problem of modeling a domain, for the purposes of prediction only. One well-explored solution assumes that all continuous variables follow a joint normal distribution (e.g. [2,1]). The other approach utilizes that fact that a great deal of progress has been made in the last decade on solving the problem in domains that contain discrete categorical variables only. This approach discretizes any continuous variables as a preprocessing step using a variety of discretization techniques, sometimes sophisticated.

Approach:

I am developing a statistical test of dependence between two continuous variables, conditioned on another set of (continuous) variables. My approach does not assume any particular distribution for the continuous variables. Like some previous ones it uses discretization, but unlike any of them it looks for possible dependency at many scales simultaneously during its attempt to determine dependence. In other words, I am developing an analytical formula for the computation of the probability of dependence at all scales (or at least the important ones) between two continuous variables X and Y conditioned on a set of continuous variables S.

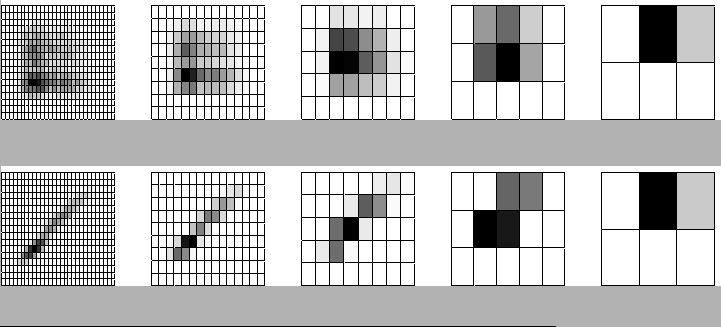
Using the ``right'' resolution (or multiple ones) can have a major effect on the dependence as determined by the discretized 2D histogram. For example, in figure 1 at the top row we see two variables, X and Y, that are independent and the histograms as they look at different resolutions starting from high at the left to low at the right. In the bottom row there is a similar array of 2D histograms of X and Y, but for when they are strongly dependent. Notice how the histograms look increasingly similar as we decrease the resolution, and completely coincide at the lowest shown resolution, despite the difference in the dependence between X and Y.

Having developed such a probabilistic dependence measure, its usefulness lies in its direct applicability in existing algorithms that discover the causal structure such as the PC, FCI [4], and GS [3] algorithms. These algorithms are completely independent of the conditional dependence test used, as long as it is a probabilistic one.

Future Work:

After developing such a conditional dependence test, I am interested in applying it to many kinds of modeling tasks that I have access to data for, from stock data to geographic information to physical law discovery in the sciences.

**Figure 1:** Effects of discretization on the appearance of dependence of two continuous variables: X-Y histograms at different resolutions of variables that are independent ( **top**) and strongly dependent ( **bottom**). The histograms look increasingly similar as we progress to lower resolutions.
$\begin{figure} \begin{center} \epsfig{file=histograms-at-multires-independent.e... ...rams-at-multires-dependent.eps}\end{center}\rule{\textwidth}{.2mm} \end{figure}$

Bibliography

About this document ...

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

The command line arguments were:
latex2html -debug -white -no_fork -no_navigation -address -split 0 -dir html -external_file dmarg dmarg.tex.