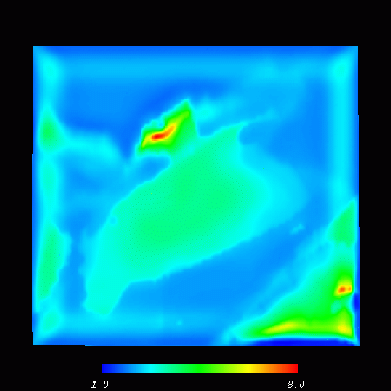
Figure 7: Surface distribution of ground motion amplification factors in the San Fernando Valley. The amplification factors have been calculated by comparing the surface to the bedrock motion.
In this section we provide timings that characterize the performance of our parallel explicit wave propagation code on the Cray T3D. We are currently using the code to study the earthquake-induced dynamics of the San Fernando Valley in Southern California. The San Fernando simulations involve meshes of up to 77 million tetrahedra and 40 million equations. The largest mesh corresponds to the case of a lowest shear wave velocity of 220 m/s and a maximum frequency of 2 Hz; the code requires nearly 16 Gb of memory and takes 6 hours to execute for 40,000 times steps on 256 processors of the Cray T3D at the Pittsburgh Supercomputing Center (PSC). Results of a typical simulation, in which the basin was subjected to a vertically-incident plane wave Ricker pulse with a central frequency of 1 Hz, indicate a factor of amplification of eight in the softer parts of the basin compared to the maximum displacement on rock. This suggests substantially greater damage in these regions. A typical result is shown in Figure 7, which depicts the amplification induced by the soft soil. Simulations of this type are essential to better predict the local site effects within soft basins such as those on which Los Angeles, San Francisco, Mexico City, and Tokyo are situated.

Figure 7:
Surface distribution of ground motion amplification factors
in the San Fernando Valley. The amplification factors have been
calculated by comparing the surface to the bedrock motion.
The relevant scenario for assessing the performance of our earthquake simulations as the number of processors increases is one in which the problem size increases proportionally, because unstructured PDE problems are typically memory-bound rather than compute-bound. Given a certain number of processors, we typically aim at full use of their memory; as the number of processors increases, we take advantage of their additional memory by increasing the problem size. In order to study the performance of our earthquake ground motion simulation code with increasing problem size, we have generated a sequence of increasingly-finer meshes for the San Fernando Basin. These meshes are labeled sf10, sf5, sf2, and sf1, and correspond to earthquake excitation periods of 10, 5, 2, and 1 second, respectively. Additionally, the mesh sf1b corresponds to a geological model that includes much softer soil in the top 30m, and thus necessitates an even finer mesh. Note that mesh resolution varies with the inverse cube of period, so that halving the period results in a factor of eight increase in the number of nodes. Characteristics of the five meshes are given in Table 1.
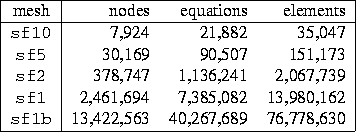
Table 1: Characteristics of San Fernando Basin meshes.
Our timings include computation and communication but exclude I/O. We exclude I/O time because in our current implementation it is serial and unoptimized, and because the T3D has a slow I/O system. I/O time involves the time at the beginning of the program to input the file produced by Parcel, as well as the time to output results every tenth time step to disk. With the availability of the Cray T3E at PSC, we plan to address parallel I/O in the future.
We begin with a traditional speedup histogram, for which the problem size is fixed and the number of processors is increased. Figure 8 shows the total time, as well as the relative time spent for communication and computation, for an earthquake ground motion simulation, as a function of the number of processors.
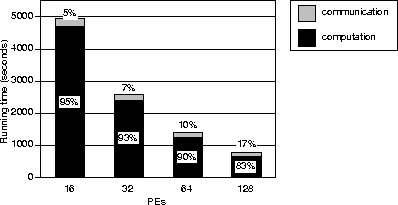
Figure 8: Timings in seconds
on a Cray T3D as a function of number of processors (PEs), excluding
I/O. The breakdown of computation and communication is shown. The mesh
is sf2, and 6000 time steps are carried out.
The mesh used for these timings is sf2. On 16 processors, the
time spent for communication is 5% of the time spent for
computation, which is quite good for such a highly irregular
problem. There are about 24,000 nodes per processor, which results in
about half the memory on each processor being used. As the number of
processors doubles, the percentage of time spent communicating
relative to computing increases, as expected. For 128 processors, the
communication time has increased to one-fifth of the total
time. However, we are only utilizing ![]() of the local
memory on a processor; practical simulations will generally exhibit
performance more like the left bar of Figure 8.
of the local
memory on a processor; practical simulations will generally exhibit
performance more like the left bar of Figure 8.
We can quantify the decrease in computation to communication ratio for
a regular mesh. Suppose there are ![]() nodes on a processor,
where P is the number of processors. Suppose further that the
regular grid is partitioned into cubic subdomains of equal size, one
to a processor. Since computation for an explicit method such as
Equation 6 is proportional to the volume of nodes in a
cube (subdomain), and communication is proportional to the number of
nodes on the surface of the cube, the computation to communication
ratio is proportional to
nodes on a processor,
where P is the number of processors. Suppose further that the
regular grid is partitioned into cubic subdomains of equal size, one
to a processor. Since computation for an explicit method such as
Equation 6 is proportional to the volume of nodes in a
cube (subdomain), and communication is proportional to the number of
nodes on the surface of the cube, the computation to communication
ratio is proportional to ![]() ,
i.e. the ratio of total nodes to surface nodes of the cube.
Thus, for fixed N, the ratio is inversely proportional to
,
i.e. the ratio of total nodes to surface nodes of the cube.
Thus, for fixed N, the ratio is inversely proportional to
![]() , at least for cubically-partitioned regular grids
with large enough numbers of nodes per processor. Clearly, it is in
our interest to keep
, at least for cubically-partitioned regular grids
with large enough numbers of nodes per processor. Clearly, it is in
our interest to keep ![]() as large as possible, if we want to
minimize communication time.
as large as possible, if we want to
minimize communication time.
Let us extend this analysis to explicit methods on unstructured
meshes. Suppose ![]() remains constant for increasing N and
P, i.e. the number of nodes per processor remains constant. Now suppose
that we have a partitioner that guarantees that the number of
interface nodes remains roughly constant as N and P
increase proportionally.
Then we can expect that the computation to communication ratio will
remain constant as the problem size increases.
remains constant for increasing N and
P, i.e. the number of nodes per processor remains constant. Now suppose
that we have a partitioner that guarantees that the number of
interface nodes remains roughly constant as N and P
increase proportionally.
Then we can expect that the computation to communication ratio will
remain constant as the problem size increases.![]() In this case, we have a method
that scales linearly: the amount of time required to solve a problem
that is doubled in size is unchanged if we double the number of
processors. How close do we come to this ideal situation? First, we
plot the log of the computation to communication ratio against the log
of the number of processors, using the data in Figure 8. A
least-squares fit yields a line with slope
In this case, we have a method
that scales linearly: the amount of time required to solve a problem
that is doubled in size is unchanged if we double the number of
processors. How close do we come to this ideal situation? First, we
plot the log of the computation to communication ratio against the log
of the number of processors, using the data in Figure 8. A
least-squares fit yields a line with slope ![]() . For a regular grid
with perfect partitioners, we have seen in the previous paragraph that
this slope should be
. For a regular grid
with perfect partitioners, we have seen in the previous paragraph that
this slope should be ![]() . This suggests that the idealized
analysis is roughly applicable here.
. This suggests that the idealized
analysis is roughly applicable here.
Next, let us attempt to hold the number of nodes per processor roughly
constant, and examine the aggregate performance of the machine as the
problem size increases. It is difficult to maintain a constant value
of ![]() , since processors are available in powers of two on the
T3D. However, we can still draw conclusions about scalability. Figure
9 shows the aggregate performance of our code
on the T3D
, since processors are available in powers of two on the
T3D. However, we can still draw conclusions about scalability. Figure
9 shows the aggregate performance of our code
on the T3D
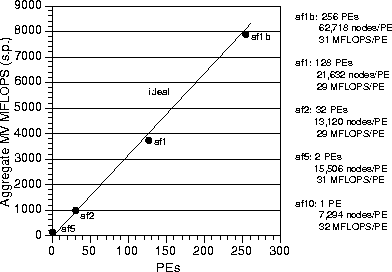
Figure 9: Aggregate performance on Cray T3D
as a function of number of processors (PEs). Rate measured for
matrix-vector (MV) product operations (which account for 80% of the
total running time and all of the communication) during 6000 times
steps.
in megaflops per second, as a function of number of processors (and, implicitly, problem size). Megaflops are those that are sustained by matrix-vector product operations (which account for 80% of the total running time and all of the communication) during a San Fernando simulation, exclusive of I/O. This figure shows nearly ideal scalability, which is defined as the single processor performance multiplied by the number of processors. These results show that excellent performance is achievable, despite the highly heterogeneous mesh. This behavior requires a partitioner that keeps the number of interface nodes relatively constant for problem size that increases concomitantly with number of processors.
An even better measure of scalability is to chart the time taken per
time step per node. If the algorithm/implementation/hardware
combination is scalable, we expect that the time taken will not change
with increasing problem size. Not only must the partitioner produce
``scalable'' partitions for this to happen, but in addition the PDE
solver must scale linearly with N. This happens when the work
per time step is ![]() .
This is obvious from the
iteration of Equation
6--vector sums, diagonal matrix inversions, and sparse
matrix-vector multiplies require
.
This is obvious from the
iteration of Equation
6--vector sums, diagonal matrix inversions, and sparse
matrix-vector multiplies require ![]() operations.
operations.
Figure 10 depicts the trend in unit wall clock time as the number of processors is increased. Unit wall clock time is measured as microseconds per time step per average number of node per processor, which includes all computations and communications for all time steps, but excludes disk I/O. As we have said above, for a truly scalable algorithm/implementation/hardware system, this number should remain constant as problem size increases with increasing processors.
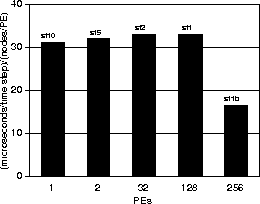
Figure: T3D wall-clock time in microseconds per
time step per average number of nodes per processor (PE), as a
function of number of processors. This figure is based on an entire
6000 time step simulation, exclusive of I/O. The sf1b result is
based on a damping scheme in which ![]() in Equation
5 so that only one matrix-vector product is
performed at each time step.
in Equation
5 so that only one matrix-vector product is
performed at each time step.
The figure demonstrates that we are close to this ideal. Ultimately, wall clock time per node per time step is the most meaningful measure of scalable performance for our application, since it is a direct indicator of the ability to solve our ultimate target problems, which are an order of magnitude larger than the San Fernando Basin problem we have described in this paper.