As we have seen, seismic wave propagation problems place special demands on mesh generators, including the need for tight control over mesh resolution and aspect ratio, and the need to support extremely large problem sizes. We have developed a fast, stable, and efficient meshing algorithm for generating very large scale meshes, suitable for the large basins we target. Since repeated computations will be performed with a single mesh (one or two dozen earthquake scenarios, each involving thousands of time steps), we have decided to generate and partition each mesh sequentially. However, care must be taken in designing and implementing efficient algorithms for these steps, lest they become bottlenecks.
Mesh generation begins with a database of the material properties of
the soil and rock within and around a particular basin. These material
properties--the shear wave velocity, the dilatational wave velocity,
and the density--are estimated throughout the basin from soil
borings, from geological records, and from seismic prospecting
studies. Figure 1 shows the variation in shear wave
velocity at a depth of three meters from the valley fill surface in a
region surrounding the San Fernando Valley in Southern California. The
material property model on which this image is based was provided by
H. Magistrale and S. Day at San Diego State University
[13].
The figure shows a variation in shear wave velocity of at least a
factor of seven. Since element width is inversely proportional to
velocity, a regular grid method can have up to ![]() times more
points per unit volume than an unstructured mesh for this material
model.
times more
points per unit volume than an unstructured mesh for this material
model.
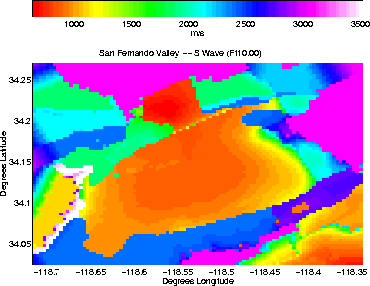
Figure 1:
Surface distribution of shear wave velocity in the San Fernando
Valley.
The meshing algorithm comprises two steps. First, we generate an octree that resolves the local wavelength of shear waves. The wavelength is known from the shear wave velocity and the frequency of excitation. Based on numerical experiments with homogeneous problems and on some theoretical analysis, we have found that 8-10 nodes per wavelength is sufficient for ``engineering'', or 95%, accuracy when using linear finite elements. (In Section 3.4 we make precise what we mean by 95% accuracy.) When constructing the octree, we enforce the rule that adjacent cells may not differ in edge length by more than a factor of two, producing a balanced octree. This is crucial for producing elements with bounded aspect ratios. Bounding the aspect ratio of elements is important because aspects ratios far from one lead to poorly conditioned stiffness matrices, which can lead to instability in time integration.
Once a balanced octree is created such that no cell is wider than one-tenth the length of the wave that passes through it, a finite element node is placed at each cell vertex. Figure 2 depicts the nodes generated by the balanced octree for

Figure 2:
Nodal distribution for the San Fernando Valley. Node generation is
based on an octree method that locally resolves the elastic
wavelength. The node distribution here is a factor of 12 coarser in
each direction than the real one used for simulation, which is too
fine to be shown, and appears solid black when displayed. However, the
relative resolution between soft soil regions and rock illustrated
here is similar to that of the 13 million node model we use for
simulations.
the San Fernando Basin properties of Figure
1. This set of
nodes is then triangulated (more properly, tetrahedralized)
according to the Delaunay criterion.![]() Figure
3
Figure
3

Figure 3:
Tetrahedral element mesh of the San Fernando Valley. Maximum
tetrahedral aspect ratio is 5.5. Again, the mesh is much coarser than
those used for simulation, for illustration purposes.
shows the resulting mesh of tetrahedra. Delaunay tetrahedralization is performed by a straightforward implementation of the Bowyer/Watson incremental algorithm [5, 23], which constructs a triangulation by adding one node at a time and locally adjusting the mesh to maintain the Delaunay criterion.
We have found that the Bowyer/Watson algorithm is occasionally sensitive to floating-point roundoff error; tetrahedral mesh generation can fail dramatically because of roundoff when processing near-degenerate geometric features. Such failures became increasingly common for us as the size of our meshes grew. To overcome this problem, we have developed a method for fast exact arithmetic that is particularly well-suited for certain tests that arise in computational geometry codes [19]. Our method is used to construct predicates that determine whether a point falls to the left or right side of a line, or whether a point falls inside or outside a sphere. These predicates are adaptive in the sense that they only use exact arithmetic to the extent it is needed to ensure a correct answer. Hence, if a point falls very close to a line, high precision arithmetic may be needed to resolve which side of the line it falls on; if a point is far from a line, approximate arithmetic will suffice, so the test can be performed quickly. Because the latter case is far more common, our exact arithmetic predicates are on average only slightly slower than ordinary, nonrobust floating-point predicates, and our Delaunay tetrahedralization code runs quickly while ensuring the integrity of its results.
Our use of the Delaunay tetrahedralization of the vertices of a balanced octree guarantees that element aspect ratios are bounded, and that element sizes are chosen appropriately so that wavelengths are sufficiently resolved without unnecessary resolution (provided the material properties do not vary too rapidly).
We have used our mesh generator to create a mesh of the San Fernando Basin with a 220 m/s shear wave velocity in the softest soil for an earthquake with a highest frequency of 2 Hz. The mesh contains 77 million tetrahedra and 13 million nodes, and was generated in 13 hours on one processor of a DEC 8400, requiring 7.7 Gb of memory. It has a maximum aspect ratio of 5.5 and exhibits a spatial resolution variability of an order of magnitude. This mesh is perhaps the largest unstructured mesh generated to date.