References

1
K. Aki. Local site effect on ground motion. In J. Lawrence Von Thun, editor, Earthquake Engineering and Soil Dynamics. II: Recent Advances in Ground-Motion Evaluation, pages 103-155. ASCE, 1988.

2
H. Bao, J. Bielak, O. Ghattas, L. F. Kallivokas, D. R. O'Hallaron, J. R. Shewchuk and J. Xu. Earthquake ground motion modeling on parallel computers. In Proceedings of Supercomputing '96, November 1996.

3
J. P. Bardet and C. Davis. Engineering observations on ground motions at the Van Norman Complex after the 1994 Northridge Earthquake. Bull. Seism. Soc. Am. 86(1B) (1996) S333-S349.

4
J. Bielak and P. Christiano. On the effective seismic input for nonlinear soil-structure interaction systems. Earthq. Eng. Struct. Dyn. 12 (1984) 107-119.

5
A. Bowyer. Computing Dirichlet tessellations. Computer Journal, 24(2) (1981) 162-166.

6
M. G. Cremonini, P. Christiano, and J. Bielak. Implementation of effective seismic input for soil-structure interaction systems. Earthq. Eng. Struct. Dyn. 16 (1988) 615-625.

7
A. Feldmann, O. Ghattas, J. R. Gilbert, G. L. Miller, D. R. O'Hallaron, E. J. Schwabe, J. R. Shewchuk, and S.-H. Teng. Automated parallel solution of unstructured PDE problems. To appear. Available from http://www.cs.cmu.edu/afs/cs.cmu.edu/project/quake/public /papers/pde.color.ps.

8
A. Frankel and J. E. Vidale. A three-dimensional simulation of seismic waves in the Santa Clara Valley, California from a Loma Prieta aftershock. Bull. Seism. Soc. Am. 82 (1992) 2045-2074.

9
R. W. Graves. Modeling three-dimensional site response effects in the Marina District Basin, San Francisco, California. Bull. Seism. Soc. Am. 83 (1993) 1042-1063.

10
S. Hartzell, A. Leeds, A. Frankel, and J. Michael. Site response for urban Los Angeles using aftershocks of the Northridge earthquake. Bull. Seism. Soc. Am. 86(1B) (1996) S168-S192.

11
H. Kawase and K. Aki. A study on the response of a soft basin for incident S, P, and Rayleigh waves with special reference to the long duration observed in Mexico City. Bull. Seism. Soc. Am. 79 (1989) 1361-1382.

12
H.-L. Liu and T. Heaton. Array analysis of the ground velocities and accelerations from the 1971 San Fernando, California, earthquake. Bull. Seism. Soc. Am. 74 (1996) 1951-1968.

13
H. Magistrale, K. L. McLaughlin, and S. M. Day. A geology-based 3-D velocity model of the Los Angeles Basin sediments. Bull. Seism. Soc. Am. 86 (1996) 1161-1166.

14
K. L. McLaughlin and S. M. Day. 3D elastic finite difference seismic wave simulations. Computers in Physics, Nov/Dec 1994.

15
G. L. Miller, S.-H. Teng, W. Thurston, and S. A. Vavasis. Automatic mesh partitioning. In A. George, J. Gilbert, and J. Liu, editors, Graph Theory and Sparse Matrix Computation, volume 56 of The IMA Volumes in Mathematics and its Application, pages 57-84. Springer-Verlag, 1993.

16
K. B. Olsen and R. J. Archuleta. Three-dimensional simulation of earthquakes on the Los Angeles Fault System. Bull. Seism. Soc. Am. 86 (1996) 575-596.

17
K. B. Olsen, R. J. Archuleta, and J. R. Matarese. Magnitude 7.75 earthquake on the San Andreas fault: Three-dimensional ground motion in Los Angeles. Science 270(5242) (1995) 1628-1632.

18
F. J. Sánchez-Sesma and F. Luzón. Seismic response of three-dimensional valleys for incident P, S, and Rayleigh waves. Bull. Seism. Soc. Am. 85 (1995) 269-284.

19
P. Spudich and M. Iida. The seismic coda, side effects, and scattering in alluvial basins studied using aftershocks of the 1986 North Palm Springs, California earthquake as source arrays. Bull. Seism. Soc. Am. 83 (1993) 1721-1724.

20
J. R. Shewchuk. Robust adaptive floating-point geometric predicates. In Proceedings of the Twelfth Annual Symposium on Computational Geometry, pages 141-150. Association for Computing Machinery, May 1996.

21
J. R. Shewchuk. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator. In First Workshop on Applied Computational Geometry, pages 124-133. Association for Computing Machinery, May 1996.

22
J. R. Shewchuk and O. Ghattas. A compiler for parallel finite element methods with domain-decomposed unstructured meshes. In D, E. Keyes and J. Xu, editors, Domain Decomposition Methods in Scientific and Engineering Computing, volume 180 of Contemporary Mathematics, pages 445-450. American Mathematical Society, 1994.

23
H. K. Thio and H. Kanamori. Source complexity of the 1994 Northridge Earthquake and its relation to aftershock mechanisms. Bull. Seism. Soc. Am. 86(1B) (1996) S84-S92.

24
J. E. Vidale and D. V. Helmberger. Elastic finite-difference modeling of the 1971 San Fernando, California, earthquake. Bull. Seism. Soc. Am. 78 (1988) 122-141.

25
D. F. Watson. Computing the n-dimensional Delaunay tessellation with application to Voronoï polytopes. Computer Journal 24(2) (1981) 167-172.

List of Tables

  

Table 1: Source characteristics.

  

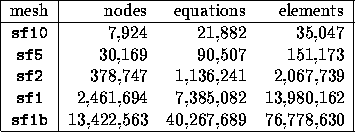
Table 2: Characteristics of San Fernando Basin meshes.

List of Figures

  

Figure 1: The Archimedes system.

 

   Click to take a close look (Same for figures below)

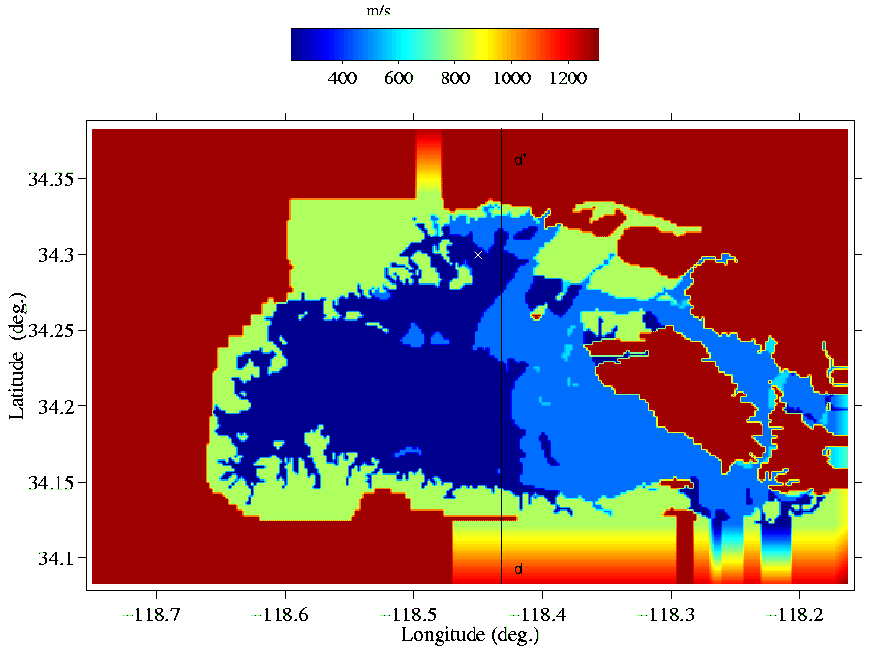
Figure 2: Near-surface distribution of shear-wave velocity in the San Fernando Valley; actual depth is 1m.

  

Figure 3: Nodal distribution for the San Fernando Valley. Node generation is based on an octree method that locally resolves the elastic wavelength. The node distribution shown here is a factor of 12 coarser in each direction than the real one used for simulation, which is too fine to be shown, and appears solid black when displayed. However, the relative resolution between soft soil regions and rock illustrated here is similar to that of the 13 million node model we use for simulations.

  

Figure 4: Tetrahedral element mesh of the San Fernando Valley. Maximum tetrahedral aspect ratio is 5.5. Again, for illustration purposes, the mesh shown is much coarser than those used for simulation.

  
Figure 5: Mesh partitioned for 64 subdomains.

  

Figure 6: Communication graph for the partitioned element mesh depicted in Fig. 5.

 

   (Click to take a close look.)

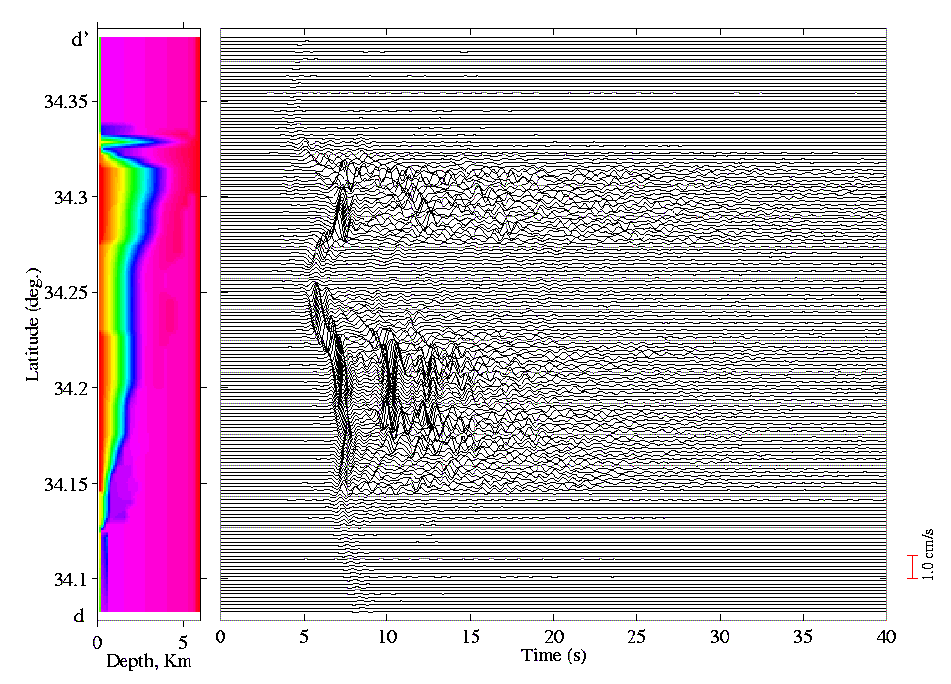
Figure 7: Horizontal surface velocity seismogram of the E-W component along the d-d axis shown in Fig. 2.

 

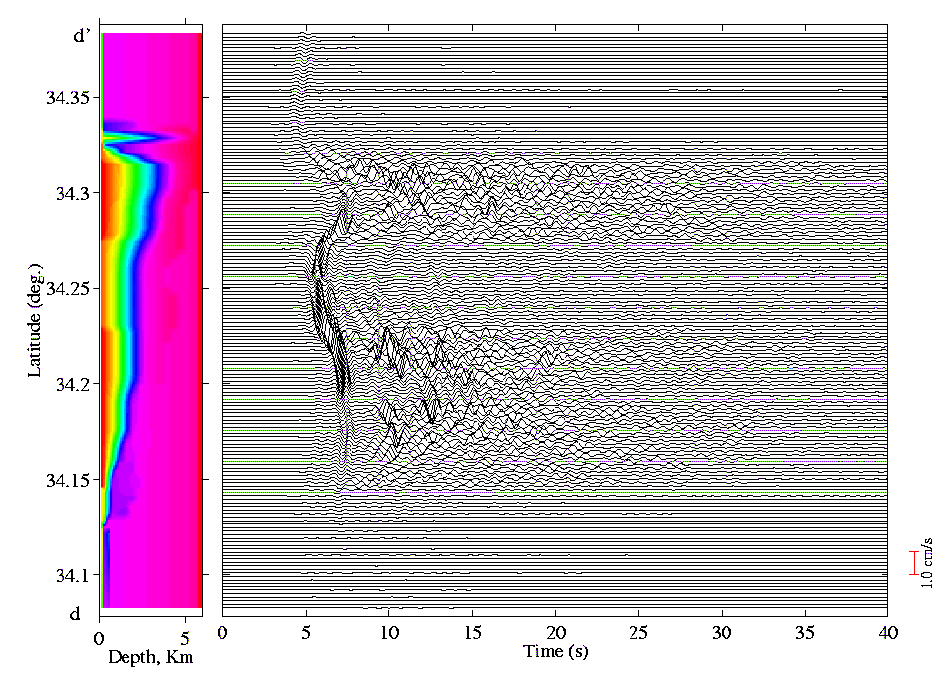   (Click to take a close look.)

Figure 8: Horizontal surface velocity seismogram of the N-S component along the d-d axis shown in Fig. 2.

 

   (Click to take a close look.)

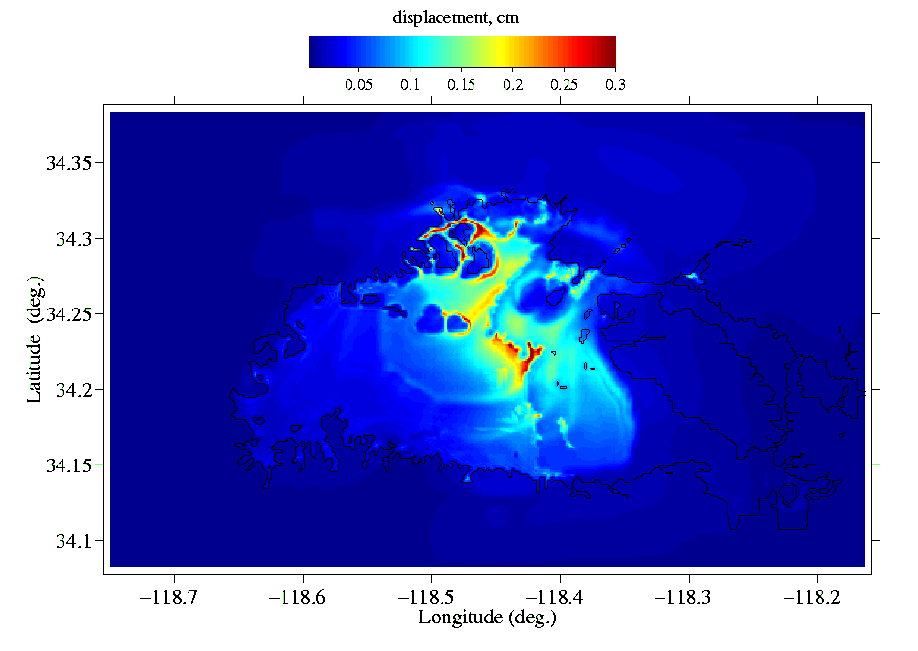
Figure 9: Distribution of maximum horizontal surface displacement.

 

   (Click to take a close look.)

Figure 10: Surface distribution of the amplitude of the Fourier Transform of the E-W displacement component for a frequency of 1.45Hz.

 

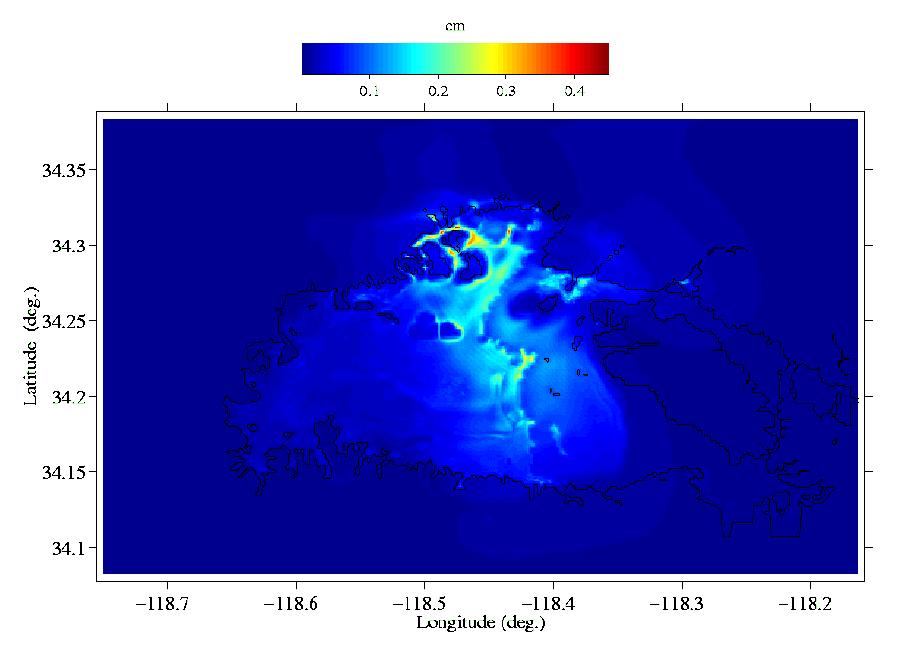   (Click to take a close look.)

Figure 11: Displacement response spectrum for a simple oscillator with 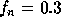Hz and 5% critical damping.

 

   (Click to take a close look.)

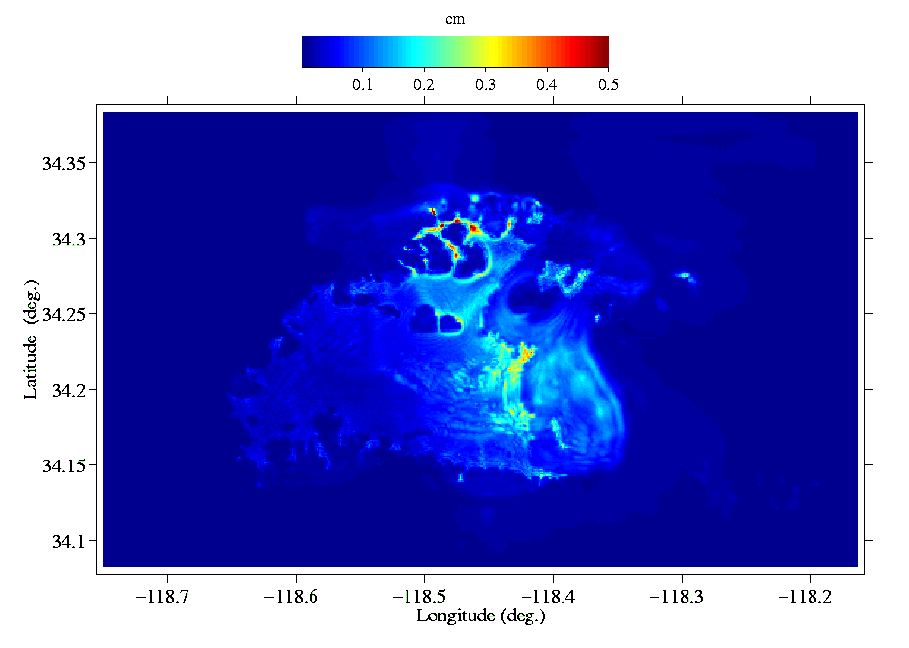
Figure 12: Displacement response spectrum for a simple oscillator with 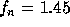Hz and 5% critical damping.

  

Figure 13: Timings in seconds on a Cray T3D as a function of number of processors (PEs), excluding I/O. The breakdown of computation and communication is shown. The mesh is sf2, and 6000 time steps are carried out.

  

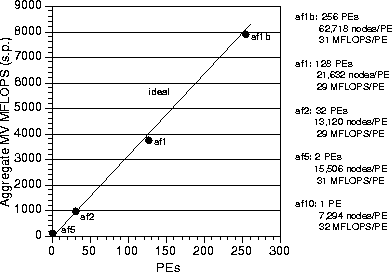
Figure 14: Aggregate performance on Cray T3D as a function of number of processors (PEs). Rate measured for matrix-vector (MV) product operations (which account for 80% of the total running time and all of the communication) during 6000 times steps.

End of List

  
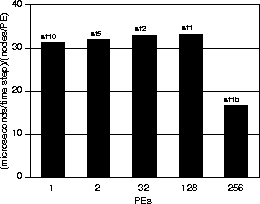
Figure 15: T3D wall-clock time in microseconds per time step per average number of nodes per processor (PE), as a function of number of processors. This figure is based on an entire 6000 time step simulation, exclusive of I/O. The sf1b result is based on a damping scheme in which in Eq. 6 so that only one matrix-vector product is performed at each time step.