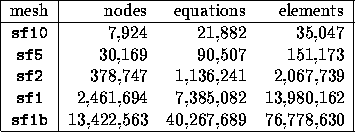
We next discuss the performance of our parallel explicit wave propagation code on the Cray T3D. The relevant scenario for assessing the performance of our earthquake simulations as the number of processors increases is one in which the problem size increases proportionally, because unstructured PDE problems are typically memory-bound rather than compute-bound. Given a certain number of processors, we typically aim at full use of their memory; as the number of processors increases, we take advantage of their additional memory by increasing the problem size. In order to study the performance of the code with increasing problem size, we have generated a sequence of increasingly-finer meshes for the San Fernando Basin. These meshes are labeled sf10, sf5, sf2, and sf1, and correspond to earthquake excitation periods of 10, 5, 2, and 1 second, respectively, and a minimum shear wave velocity of 500m/s. Additionally, the mesh sf1b corresponds to the geological model used for the simulations described in the preceding section, which includes much softer soil in the top 30m, and thus necessitates an even finer mesh. Note that mesh resolution varies with the inverse cube of the excitation period, so that halving the period results in a factor of eight increase in the number of nodes. Characteristics of the five meshes are given in Table 2.
Table 2: Characteristics of San Fernando Basin meshes.
Our timings include computation and communication but exclude I/O. We exclude I/O time because in our current implementation it is serial and unoptimized, and because the T3D has a slow I/O system. I/O time involves the time at the beginning of the program to load and read the input file produced by the parceling operation, as well as the time to output results every 30th time step to disk. With the availability of the Cray T3E at PSC, we plan to address parallel I/O in the future.
We begin with a traditional speedup histogram, for which the problem
size is fixed and the number of processors is increased.
Figure 13 shows the total time, as well as the relative
time spent for communication and computation, for an earthquake ground
motion simulation, as a function of the number of processors. The
mesh used for these timings is sf2. On 16 processors, the time
spent for communication is 5% of the time spent for computation,
which is quite good for such a highly irregular problem. There are
about 24,000 nodes per processor, which results in about half the
memory on each processor being used. As the number of processors
doubles, the percentage of time spent communicating relative to
computing increases, as expected. For 128 processors, the
communication time has increased to one-fifth of the total time.
However, we are only utilizing 
of the local memory on a
processor; practical simulations will generally exhibit performance
more like the left bar of Fig. 13.
Figure 13: Timings in seconds
on a Cray T3D as a function of number of processors (PEs), excluding
I/O. The breakdown of computation and communication is shown. The mesh
is sf2, and 6000 time steps are carried out.
We can quantify the decrease in computation to communication ratio for
a regular 
mesh. Suppose there
are 
nodes on a processor, where P is the number of
processors. Suppose further that the regular grid is partitioned into
cubic subdomains of equal size, one to a processor. Since computation
for an explicit method such as Eq. 7 is proportional to
the volume of nodes in a cube (subdomain), and communication is
proportional to the number of nodes on the surface of the cube, the
computation to communication ratio is proportional to
, i.e. the ratio of total nodes to surface
nodes of the cube. Thus, for fixed N, the ratio is inversely
proportional to 
, at least for cubically-partitioned regular
grids with large enough numbers of nodes per processor. Clearly, it is
in our interest to keep 
as large as possible, if we want to
minimize communication time.
Consider now the case of unstructured, rather than regular,
meshes. Suppose that 
remains constant for increasing N and
P, i.e. the number of nodes per processor remains constant. Now
suppose that we have a partitioner that guarantees that the number of
interface nodes remains roughly constant as N and P increase
proportionally. Then we can expect that the computation to
communication ratio will remain constant as the problem size
increases. In this case, we have a method that scales linearly: the amount of time
required to solve a problem that is doubled in size is unchanged if we
double the number OCof processors. Let us attempt to hold the number of nodes per processor roughly
constant, and examine the aggregate performance of the machine as the
problem size increases. It is difficult to maintain a constant value
of 
, since processors are available in powers of two on the T3D.
However, we can still draw conclusions about scalability.
Figure 14 shows the aggregate performance of our
code on the T3D in megaflops per second, as a function of number of
processors (and, implicitly, problem size). Megaflops are those that
are sustained by matrix-vector product operations (which account for
80% of the total running time and all of the communication) during a
San Fernando simulation, exclusive of I/O. This figure shows nearly
ideal scalability, which is defined as the single processor
performance multiplied by the number of processors. These results show
that excellent performance is achievable, despite the highly
multiscale mesh. This behavior requires a partitioner that keeps the
number of interface nodes relatively constant for problem size that
increases concomitantly with number of processors.
Figure 14: Aggregate performance on Cray T3D
as a function of number of processors (PEs). Rate measured for
matrix-vector (MV) product operations (which account for 80% of the
total running time and all of the communication) during 6000 times
steps.
An even better measure of scalability is to chart the time taken per
time step per node. If the algorithm/implementation/hardware
combination is scalable, we expect that the time taken will not change
with increasing problem size. Not only must the partitioner produce
``scalable'' partitions for this to happen, but in addition the PDE
solver must scale linearly with N. This happens when the work per
time step is 
. This is obvious from the iteration of
Eq. 7--vector sums, diagonal matrix inversions, and
sparse matrix-vector multiplies require 
operations.
Figure 15 depicts the trend in unit wall clock time as the number of processors is increased. Unit wall clock time is measured as microseconds per time step per average number of node per processor, which includes all computations and communications for all time steps, but excludes disk I/O. As we have said above, for a truly scalable algorithm/implementation/hardware system, this number should remain constant as problem size increases with increasing processors. The figure demonstrates that we are close to this ideal. Ultimately, wall clock time per node per time step is the most meaningful measure of scalable performance for our application, since it is a direct indicator of the ability to solve our ultimate target problems, which are an order of magnitude larger than the San Fernando Basin problem we have described in this paper.
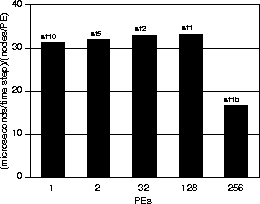
Figure 15: T3D wall-clock time in microseconds per time step per
average number of nodes per processor (PE), as a function of number of
processors. This figure is based on an entire 6000 time step
simulation, exclusive of I/O. The sf1b result is based on a
damping scheme in which 
in Eq. 6 so
that only one matrix-vector product is performed at each time step.
