



Next: About this document ...
Up: Bibliography
Previous: Moment matching algorithm by
Contents
Properties of Markovian arrival processes
Below, we summarize some of the basic properties of the MAP.
First, the set of MAPs is quite broad and, in theory, any stationary point
process can be approximated arbitrarily closely by a MAP.
Proposition 6
[12]
The set of MAPs is dense in the set of all the stationary point processes.
Second, the set of MAPs is closed under some operations. In particular,
a superposition of two independent MAPs is a MAP.
Third, the average rate of events and the marginal distribution of the inter-event time
of a MAP have simple mathematical expressions.
Since the marginal distribution of the inter-event time in a MAP is a PH distribution,
its moments, density function, and distribution function can be calculated via Proposition 4.
The variability of a point process can be characterized by the covariance
of the inter-event times or the index of dispersion for intervals.
The index of dispersion for intervals, IDI( ), of a MAP is defined
by
), of a MAP is defined
by
where  is the sum of the first
is the sum of the first  inter-event times of the MAP.
Observe that IDI(
inter-event times of the MAP.
Observe that IDI( ) is the ratio of the variance of
) is the ratio of the variance of  to the corresponding variance of a Poisson process with the same rate.
The MAP have a convenient mathematical expressions for the covariance and the index of dispersion for intervals.
to the corresponding variance of a Poisson process with the same rate.
The MAP have a convenient mathematical expressions for the covariance and the index of dispersion for intervals.
Proposition 9
[7,92]
Consider MAP(
 ) with the fundamental rate
) with the fundamental rate 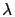 .
Recall the vectors,
.
Recall the vectors, 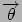 and
and  , of the MAP defined in Proposition 8.
The covariance between the two inter-event times separated by
, of the MAP defined in Proposition 8.
The covariance between the two inter-event times separated by  events of the MAP is given by
events of the MAP is given by
The IDI( ) of the above MAP is given by
) of the above MAP is given by
Finally, a MAP can be translated into a counting process, i.e., the number of events by time  ,
,  .
The MAP has a simple
.
The MAP has a simple  -transform of
-transform of  , and this leads
to a convenient mathematical expression for the index of dispersion for counts,
which characterizes the variability of a MAP via the variability of
, and this leads
to a convenient mathematical expression for the index of dispersion for counts,
which characterizes the variability of a MAP via the variability of  .
The index of dispersion for counts, IDC(
.
The index of dispersion for counts, IDC( ), of the MAP is defined by
), of the MAP is defined by
Observe that IDC( ) is the ratio of the variance of
) is the ratio of the variance of  to the corresponding variance of a Poisson process with the same rate.
to the corresponding variance of a Poisson process with the same rate.




Next: About this document ...
Up: Bibliography
Previous: Moment matching algorithm by
Contents
Takayuki Osogami
2005-07-19
![]() ) distribution,
where
) distribution,
where
![]() ), of a MAP is defined
by
), of a MAP is defined
by
![]() ) of the above MAP is given by
) of the above MAP is given by

![]() ,
, ![]() .
The MAP has a simple
.
The MAP has a simple ![]() -transform of
-transform of ![]() , and this leads
to a convenient mathematical expression for the index of dispersion for counts,
which characterizes the variability of a MAP via the variability of
, and this leads
to a convenient mathematical expression for the index of dispersion for counts,
which characterizes the variability of a MAP via the variability of ![]() .
The index of dispersion for counts, IDC(
.
The index of dispersion for counts, IDC(![]() ), of the MAP is defined by
), of the MAP is defined by
![]() ) of the above MAP is given by
) of the above MAP is given by