Mihai Budiu -- mihaib+@cs.cmu.edu, http://www.cs.cmu.edu/~mihaib/
1 iunie 1997
În ultimii ani cercetarea în domeniul algoritmilor a apucat pe niște căi extrem de interesante și foarte deosebite de cele tradiționale. Unele dintre aceste căi erau prefigurate de descoperiri făcute cu multă vreme în urmă, dar nu fuseseră urmate sistematic. Altele sunt de dată recentă. Metodele noi încearcă să depășească criza în care intraseră metodele de rezolvare a anumitor clase de probleme (cum ar fi cele NP-complete), sau să facă față unor probleme de naturi diferită: informație incompletă (de exemplu cînd trebuie luate decizii fără a cunoaște cererile ulterioare), informație distribuită (într-o rețea de calculatoare), informație ascunsă (în criptografie), etc. Acest articol își propune să ilustreze foarte sumar cîteva dintre noile direcții de acțiune.
În această secțiune vom face o scurtă recapitulare a principalelor noțiuni care ne sunt necesare în înțelegerea celorlalte părți. Acestea sunt bine-cunoscute din studiul algoritmilor clasici, astfel încît cititorul informat le poate sări fără pierderi de informație. Tratarea va fi desigur sumară; cititorul ne-informat este invitat să parcurgă cărți clasice în domeniu pentru o discuție mai amplă. Pe de altă parte aceste noțiuni nu sunt simple, și foarte arar sunt tratate într-adevăr riguros. Deși expunerea de față va fi sumară, sper că nu va păcătui și prin lipsă de corectitudine.
Un algoritm este o descriere a unui proces de calcul, care din niște date inițiale produce niște rezultate interesante. Descrierea se face în termenii unor operații elementare (operații aritmetice, comparații, decizii, etc.).
Aparent modul în care rezolvăm problemele depinde de operațiile pe care le avem la-ndemînă. În cazul acesta se ivește natural întrebarea dacă anumite operații nu sunt mai expresive decît altele. Acest lucru este adevărat, după cum se vede și din proliferarea limbajelor de programare; un astfel de limbaj definește practic o colecție de operații elementare.
Se poate demonstra absolut riguros, că în oarecare măsură alegerea limbajului este irelevantă, pentru că, din momentul în care avem un limbaj suficient de expresiv, putem simula cu ajutorul lui operațiile care se fac în toate celelalte limbaje cunoscute. Astfel, toate formalismele care exprimă procese de calcul au fost demonstrate ca fiind echivalente ca putere expresivă (limbajele de programare, lambda calculul, funcțiile recursive, gramaticile de tip 0, mașinile Turing: toate aceste metode de calcul pînă la urmă sunt echivalente).
Din acest motiv ne putem fixa asupra unui limbaj anume, fără a pierde nimic din generalitatea expunerii. Voi folosi pentru exemplele din acest articol un limbaj foarte simplu, asemănător cu limbajele obișnuite de programare. Limbajul (``guarded command language'') a fost introdus de Dijkstra, și se bazează pe folosirea gărzilor, care sunt niște simple expresii booleene. Gărzile sunt folosite pentru a descrie două construcții: bucla do și instrucțiunea if. Astfel:
do garda_1 -> instructiune_1 [] garda_2 -> instructiune_2 ... [] garda_n -> instructiune_n od
funcționează astfel: gărzile se evaluează; dacă:
Dacă programatorul vrea să fie sigur ce instrucțiune se execută, nu are decît să construiască programul în așa fel încît două gărzi sa nu fie adevărate simultan.
Construcția do este asemănătoare cu un while urmat de un switch din C, dar este mai ușor de folosit. Oricum, este evident că este la fel de expresivă.
Folosim apoi construcția if pe post de switch (case din Pascal):
if garda_1 -> instructiune_1 [] garda_2 -> instructiune_2 ... [] garda_n -> instructiune_n fi
Semnificația este foarte asemănătoare cu a lui do. Astfel:
Mai folosim și atribuirea paralelă:
v_1, v_2, ..., v_n := e_1, e_2, ..., e_n
Prin care expresiile din dreapta sunt toate evaluate și atribuite simultan variabilelor din stînga. Din cauza asta schimbul valorilor a două variabile se poate face cu
x, y := y, x
care operație nu este echivalentă nici cu
x := y y := x
și nici cu
y := x x := y
Ca să ne familiarizăm cu limbajul, să scriem un mic algoritm, care, dîndu-se o valoare x și un vector a cu n elemente, partiționează vectorul în așa fel încît valorile mai mici ca x ajung în stînga, cele mai mari în dreapta, iar toate cele egale cu x sunt contigue, undeva între celelalte două (acesta este un fragment din quicksort):
l, r, m := 1, n, 1 do a[m] = x -> m := m+1 [] a[m] < x -> a[l], a[m], l, m := a[m], a[l], l+1, m+1 [] (a[m] > x) and (m < r) -> a[r], a[m], r := a[m], a[r], r-1 [] a[r] > x -> r := r-1 od
Acest algoritm operează asupra vectorului a menținînd următorul invariant (o relație care este întotdeauna adevărată):
| < | = | ? | > | a
-----------------------------------------------------------
1 ^ ^ ^ n
l m r
Variabilele l, m și r sunt indici în vectorul a. Tot ce e la stînga lui l e mai mic decît x, tot ce este cuprins între l (inclusiv) și m (exclusiv) este egal cu x, iar tot ce se află la dreapta lui r este mai mare ca x. Elementele dintre m și r sunt încă ne-explorate. Această relație este adevărată atunci cînd algoritmul începe, din modul în care se inițializează variabilele, și rămîne adevărată la fiecare parcurgere a buclei do, după cum se poate verifica. Bucla se termină cînd toate gărzile sunt adevărate, ceea ce se poate doar dacă m = r, deci dacă zona ne-explorată s-a redus la 0.
Limbajul acesta nu este foarte eficace pentru a scrie sisteme de operare, dar pentru a exprima algoritmi este foarte succint și elegant. Invariantul anterior se reduce, în cazul terminării, deci cînd m = r la
| < | = | > | a
-----------------------------------------------------------
1 ^ ^ n
l m=r
ceea ce implică și corectitudinea algoritmului, pentru că acesta este rezultatul pe care trebuia să-l obținem.
Ca să demonstrăm ca algoritmul se termină întotdeauna, independent de valorile lui x, n și a, observați că ori toate gărzile sunt false (și atunci gata), ori cel puțin o gardă este adevărată, și atunci fie m crește, fie r scade. Cum întotdeauna trebuie să avem m < r, bucla se poate parcurge de cel mult n ori înainte de terminare.
Observați că acest algoritm este nedeterminist, pentru că dacă a[r] > x poate face două alegeri. Interesant este că rezultatul final nu depinde de care operație este făcută, pentru că ambele operații păstrează invariantul indicat și reprezintă un progres. De asemenea, observați că algoritmul rămîne corect dacă eliminăm ultima linie din do, și în acest caz devine și determinist!
O distincție foarte importantă pe care trebuie s-o facem este între clasa de probleme pe care o rezolvă un algoritm, și instanțele specifice ale acelei probleme. De exemplu, algoritmul descris mai sus rezolva toate problemele care conțin un vector de n elemente și o valoare x, aducînd vectorul la forma indicată. Cînd rulăm acest algoritm însă, o facem cu o instanță particulară a problemei: de exemplu vectorul cu n=5 elemente a = [1, 2, 5, 3, 2], și cu x = 2.
Distincția este esențială, mai ales cînd vrem să evaluăm eficacitatea unui algoritm. Măsurarea performanței unui algoritm cu ceasul în mînă nu este o operație foarte semnificativă, dacă algoritmul va rezolva și alte instanțe ale problemei decît cea măsurată. Dacă algoritmul de mai sus, implementat pe un anumit calculator, rezolvă instanța indicată în 5 milisecunde, asta nu spune absolut nimic despre viteza lui pentru o cu totul altă instanță. Dacă vrem să evaluăm calitatea algoritmilor trebuie să găsim o metodă care nu depinde de instanțe, ci de problema însăși.
O întrebare pe care ne-o putem imediat pune este: cît de bun este un algoritm? Nu se poate scrie un altul mai bun (care să rezolve aceeași problemă, firește)? Pentru a putea răspunde, trebuie să cădem de acord asupra unei metode prin care măsurăm calitățile unui algoritm; putem măsura timpul lui de execuție pentru o anumită problemă, sau cantitatea de memorie folosită, sau numărul de instrucțiuni care descriu programul, sau poate o altă dimensiune.
Dacă am doi algoritmi pentru aceeași problemă, atunci poate pentru anumite instanțe ale problemei unul este mai rapid, iar pentru alte instanțe celălalt. Dintre algoritmii de sortare sortarea prin selecție este preferată pentru vectori mici, iar quicksort sau heapsort pentru vectori mari. Dacă valorile din vector sunt mici, atunci le bate pe amîndouă radixsort. Și atunci, cum comparăm doi algoritmi?
Există un răspuns relativ unanim acceptat la această întrebare, dar, înainte de a-l prezenta, trebuie încă odată să spunem că acesta este doar un punct de vedere în comparație, și că în practică se pot prefera algoritmii și din alte motive. Cel mai interesant atribut al performanței a fost judecat a fi timpul de execuție al unui algoritm. Timpul este apoi asimilat cu numărul de operații elementare pe care le efectuează un algoritm pentru a rezolva o problemă.
Din păcate, chiar pentru o instanță fixată a unei probleme, numărarea instrucțiunilor executate este o sarcină foarte dificilă. Din această cauză se socotește suficient a se măsura de cîte ori se repetă instrucțiunea care se execută cel mai mult. Aceasta este instrucțiunea dominantă, și se găsește de regulă în interiorul tuturor buclelor. Numărul de repetiții al instrucțiunii dominante este o aproximație rezonabilă pentru numărul total de instrucțiuni executat de algoritm. Oricum, din moment ce nici o instrucțiune nu se mai execută atît de mult, dacă înmulțim lungimea programului cu numărul de repetiții al instrucțiunii dominante avem imediat o margine superioară pentru timpul de execuție. Vom vedea mai jos că folosirea pentru a indica complexitatea a ordinului de mărime a unei funcții face neimportant un factor multiplicativ (anume lungimea programului).
Observați că pentru instanțe diferite ale unei aceleiași probleme, numărul de instrucțiuni executat este în general diferit. De exemplu, acest scurt program, care caută un număr x în vectorul a:
i = 1 do (i <= n) and not (a[i] = x) -> i := i + 1 od
va avea un timp de execuție egal cu 1 dacă x = a[1] sau cu n dacă x nici nu apare în vector.
Este de asemenea evident că timpul de execuție depinde adesea de cantitatea datelor de intrare; în exemplele date mai sus el depinde de numărul de elemente din vectorul a.
Să recapitulăm deci: avem un algoritm care rezolvă o clasă de probleme. Pentru fiecare instanță, complexitatea algoritmului se măsoară în numărul de instrucțiuni executate pentru a rezolva acea instanță.
Noi ne dorim însă o măsură unică, globală a unui algoritm, care să-l caracterizeze, și nu complexitatea pentru fiecare instanță. Atunci procedăm astfel: alegem o valoare arbitrară care o numim mărimea datelor de intrare. Cînd algoritmul lucrează pe un vector (ca în exemplul de mai sus), o alegere posibilă este numărul de elemente. În general valoarea care caracterizează mărimea datelor de intrare arată cît de multă informație este prezentă în datele de intrare. Acesta este un lucru normal, pentru că ne putem aștepta ca atunci cînd avem mai multe date la intrare algoritmul să lucreze mai multă vreme.
În acest fel partiționăm mulțimea intrărilor în mulțimi (disjuncte) de ``mărimi'' egale. Pentru algoritmul precedent vom avea astfel probleme de ``mărime 1'': cele care au vectorul dintr-un singur element. Vom avea probleme de ``mărime k'', cu vectori de lungime k, ș.a.m.d. Firește, există mai multe instanțe cu mărimea k.
Mai departe există două metode răspîndite pentru a decide complexitatea unui algoritm pentru date de mărime fixată. Cea mai comună se cheamă: ``cel mai rău caz'' (worst-case complexity). Pe scurt: fixăm mărimea, măsurăm numărul de instrucțiuni pentru fiecare instanță de această mărime, și apoi luăm maximumul.
Complexitatea T pentru mărimea fixată n este maximumul timpilor pentru toate problemele de mărime n.
De exemplu, pentru algoritmul de căutare expus mai sus, complexitatea pentru vectori de mărime n este n, pentru instanțele în care x nu se regăsește în vector.
În acest fel complexitatea unei probleme se exprimă ca o funcție de mărimea problemei.
date de intrare P ------------------------ | instante de marime 1 | -> max timp(P) = T(1) ------------------------ | instante de marime 2 | -> max timp(P) = T(2) ------------------------ .... ------------------------ | instante de marime n | -> max timp(P) = T(n) ------------------------ ....
A doua metodă de a evalua complexitatea problemelor pentru o mărime
fixată este de a pune o distribuție de probabilitate peste
instanțele de o anumită mărime (de exemplu toate pot fi egal
probabile) și de a evalua apoi valoarea medie a variabilei aleatoare
care descrie timpul de rulare. Considerînd numai problemele de
mărime n, dacă rezolvarea problemei x va dura un timp t(x) iar
problema se va ivi cu probabilitatea p(x), atunci complexitatea
algoritmului va fi
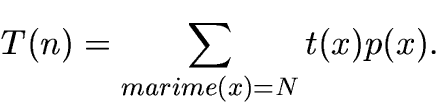
Această tehnică este mult mai rar folosită, pentru că:
Metoda cu distribuția de probabilitate a fost în general aplicată la algoritmi de căutare și sortare, dar chiar și în aceste cazuri simple rezultatele nu sunt întotdeauna facile.
De aici înainte vom presupune că folosim complexitate ``worst case''.
Cînd cineva spune ``acesta este un algoritm de complexitate n2, de fapt vrea să spună: ``pentru anumite de intrare de mărime n algoritmul execută instrucțiunea dominantă de cel mult n2 ori.'' Acest n este implicit deci dimensiunea datelor de intrare. Vom folosi și noi această literă liber, fără a mai indica sursa ei de proveniență.
Pentru că de fapt noi socotim numai numărul de repetiții al instrucțiunii dominante, și nu toate instrucțiunile executate, nu are foarte mult sens să comparăm între un algoritm cu complexitatea n și unul cu complexitate n+1. Toate instrucțiunile care nu au fost măsurate au o contribuție care să facă algoritmul cu n să dureze în realitate mai mult decît cel cu n+1. Ceea ce trebuie să comparăm de fapt este ordinul de mărime al complexității, care pune în evidență creșteri substanțial diferite. Pentru a face evident acest lucru se folosește o notație pentru ordinul de mărime al unei funcții, introdus de fizicianul Lev Davidovich Landau. Notația folosește simbolul O (``o mare'') pentru a indica mulțimea funcțiilor care cresc mai repede decît o funcție dată. Această notație compară numai funcții la limită, în creșterea lor spre infinit. Pentru a putea compara complexitatea a doi algoritmi care rezolvă o aceeași problemă în acest fel, trebuie ca ei să poată lucra cu probleme de mărimi arbitrar de mari!
Definiție: fie dată o funcție f : N --> N,
astfel încît de la un rang încolo f(n) > 0; atunci mulțimea
funcțiilor dominate de f se notează cu O(f) și se definește
astfel:

Din păcate notația se folosește în uzajul comun în mod greșit,
scriindu-se f = O(g) în loc de ![]() : O(g) este o mulțime de funcții, toate
dominate de g.
: O(g) este o mulțime de funcții, toate
dominate de g.
Din considerentele indicate, metoda preferată pentru a indica complexitatea unui algoritm este de a o face prin ordinul de mărime al funcției sale de complexitate. Din cauza că analizează această comportare spre infinit complexitatea algoritmilor se numește ``complexitate asimptotică''.
Ce înseamnă deci că un algoritm ``are o complexitate O(n log n)''? Înseamnă că pe măsură ce datele de intrare cresc în mărime ca n, numărul de operații făcut de algoritm în raport cu mărimea datelor de intrare este mai mică de n log n ori.
Astfel complexitatea asimptotică exprimă concis o limită superioară a timpului de execuție a unui algoritm. O grămadă de informație se pierde din descrierea complexității unui algoritm dînd numai ordinul de mărime:
Cu toate aceste dezavantaje, notația cu O s-a impus, și s-a dovedit în general destul de eficace pentru a caracteriza algoritmii. Proprietățile notației O sunt foarte interesante, dar depășesc cadrul acestui articol; în general sunt destul de intuitive (de exemplu: dacă f = O(g) și g = O(h), atunci f = O(h)$, etc.
În final, reluînd o observație de la începutul secțiunii, să observăm că într-adevăr n = O(n+1) și n+1 = O(n), așa că într-adevăr notația cu O aruncă termenii nesemnificativi, și faptul că am numărat numai instrucțiuni dominante nu are nici o importanță. Mai exact, este foarte ușor de arătat că timpul real de execuție a unui algoritm este O(numărul de repetiții al instrucțiunii dominante).
Am admis tacit că toate operațiile elementare se pot efectua în timp unitar, dar acest lucru poate adesea să ne inducă în eroare. De exemplu, atunci următorul algoritm, care calculează numărul 22...2, funcționează în n pași:
x, i := 2, 1 do i <= n -> x, i := x * x, i+1 od
Numărul care se obține în acest fel este extrem de lung, și este mult mai rezonabil să presupunem că operațiile cu numere iau un timp care depinde de lungimea numărului în biți.
Vom ignora însă aceste considerente ușor ezoterice, și ne vom mulțumi să presupunem că în algoritmii noștri toate operațiile pot fi făcute în timp constant.
Un algoritm rezolvă o problemă. Adesea pentru a rezolva o aceeași problemă putem folosi mai mulți algoritmi, poate cu complexități diferite. Există cel puțin 30 de metode de a sorta un șir de valori, de exemplu! Putem vorbi deci de complexitatea unui algoritm, dar și de complexitatea unei probleme. Complexitatea unei probleme este complexitatea celui mai ``rapid'' algoritm care o poate rezolva. Complexitatea unei probleme este deci o limită inferioară a eficacității cu care putem rezolva o problemă: orice algoritm care va rezolva acea problemă va fi mai complex decît complexitatea problemei.
În general este extrem de dificil de evaluat complexitatea unei probleme, pentru că rareori putem demonstra că un algoritm este cel mai bun posibil. Tabloul arată cam așa:
limita inferioara complexitatea cel mai bun
dovedita problemei algoritm cunoscut
---------|------------------?----------------------|----------------
f g
Cu alte cuvinte, putem spune: ``problema asta nu se poate face mai repede de f, și noi știm s-o rezolvăm în g''. Dar care este complexitatea reală, și care este algoritmul care rezolvă problema optim, asta foarte rar se poate spune.
Pentru o problemă atît de banală ca înmulțirea a două numere, considerînd numerele scrise în baza 2, iar mărimea lor numărul total de biți n, complexitatea celui mai bun algoritm de înmulțire cunoscut este de O(n log n log log n), dar limita inferioară dovedită este de n. Sau pentru înmulțirea a două matrici de n*n elemente: se găsesc încontinuu algoritmi din ce în ce mai buni (asimptotic vorbind), dar limita inferioară de n2 este încă departe de cel mai bun (și foarte sofisticat algoritm), care este aproximativ O(n2,3) (comparați cu algoritmul ``naiv'' imediat, care este O(n3)).
Unele probleme se pot rezolva, altele nu. De exemplu, o problemă notorie, a cărei imposibilitate este riguros demonstrată în anii '30 de către matematicianul englez Alan Turing, este de a decide dacă un program se va opri vreodată pentru o anumită instanță a datelor de intrare.
Pe de altă parte, chiar între problemele care pot fi rezolvate, teoreticienii trag o linie imaginară între problemele care au rezolvări ``rezonabil'' de rapide, și restul problemelor, care se numesc ``intratabile''.
În mod arbitrar, dar nu ne-justificabil, o problemă se numește ``intratabilă'' dacă complexitatea ei este exponențială în mărimea datelor de intrare. (Nu uitați, este vorba de complexitate ``worst-case'' asimptotică.) O problemă este ``tratabilă'' dacă putem scrie complexitatea ei sub forma unui polinom, de un grad oricît de mare.
Mulțimea tuturor problemelor de decizie (adică a problemelor la care răspunsul este da sau nu) cu complexitate polinomială se notează cu P (de la polinom). De exemplu, problema de a găsi dacă o valoare se află într-un vector este în clasa P; algoritmul exhibat mai sus este un algoritm în timp linear (O(n)) pentru a răspunde la această întrebare.
Un exemplu de problemă cu complexitate exponențială
(ne-polinomială)? Iată unul: dacă se dă o formulă logică peste
numerele reale, cu cuantificatori existențiali (![]() ) și
universali (
) și
universali (![]() ), care folosește numai operații de adunare,
comparații cu < și conectori logici (
), care folosește numai operații de adunare,
comparații cu < și conectori logici (
![]() ), este formula adevărată? (Un exemplu de formulă:
``
), este formula adevărată? (Un exemplu de formulă:
``
![]() ''). Decizia se poate face numai într-un timp exponențial în
lungimea formulei (pentru anumite instanțe), dar demonstrația nu
este de loc simplă.
''). Decizia se poate face numai într-un timp exponențial în
lungimea formulei (pentru anumite instanțe), dar demonstrația nu
este de loc simplă.
(Ca o curiozitate: există și probleme cu o complexitate
``ne-elementară'', care este mai mare decît complexitatea oricărei
probleme exponențiale. O astfel de problemă este cea de decizie a
adevărului unei formule în teoria numită S1S, sau ``teoria
monadică a succesorilor de ordinul 2''. Nu vă lăsați intimidați
de terminologie: aceasta este practic o teorie logică peste numerele
naturale, în care avem voie să scriem formule cu cuantificatori și
conectori logici, ca mai sus, dar avem și dreptul să cuantificăm
peste mulțimi. Complexitatea deciziei unei formule logice într-o
astfel de teorie este mai mare decît
![]() pentru orice k natural!)
pentru orice k natural!)
Algoritmii cu care suntem obișnuiți să lucrăm zi de zi sunt determiniști. Asta înseamnă că la un moment dat evoluția algoritmului este unic determinată, și ca instrucțiunea care urmează să se execute este unic precizată în fiecare moment. Am văzut însă că limbajul pe care l-am folosit ne permite scrierea unor algoritmi care au mai multe posibilități la un moment dat; construcția if din limbajul cu gărzi permite evaluarea oricărei instrucțiuni care are garda adevărată.
Acest tip de algoritmi este surprinzător de bogat în consecințe cu valoare teoretică. Acești algoritmi nu sunt direct aplicabili, însă studiul lor dă naștere unor concepte foarte importante.
Surprinzătoare este și definiția corectitudinii unui astfel de algoritm. Un algoritm nedeterminist este corect dacă există o posibilitate de executare a sa care găsește răspunsul corect. Pe măsură ce un algoritm nedeterminist se execută, la anumiți pași se confruntă cu alegeri nedeterministe. Ei bine, dacă la fiecare pas există o alegere, care făcută să ducă la găsirea soluției, atunci algoritmul este numit corect.
Astfel, un algoritm nedeterminist care caută ieșirea dintr-un labirint ar arăta cam așa:
do not iesire(pozitie_curenta) ->
if not perete(nord(pozitie_curenta)) ->
pozitie_curenta := nord(pozitie_curenta)
[] not perete(est(pozitie_curenta)) ->
pozitie_curenta := est(pozitie_curenta)
[] not perete(sud(pozitie_curenta)) ->
pozitie_curenta := sud(pozitie_curenta)
[] not perete(vest(pozitie_curenta)) ->
pozitie_curenta := vest(pozitie_curenta)
fi
od
Pe scurt algoritmul se comportă așa: dacă la nord nu e perete mergi încolo, sau, poate, dacă la sud e liber, mergi încolo, sau la est, sau la vest. În care dintre direcții, nu se precizează (este ne-determinat). Este clar că dacă există o ieșire la care se poate ajunge, există și o suită de aplicări ale acestor reguli care duce la ieșire.
Utilitatea practică a unui astfel de algoritm nu este imediat aparentă: în definitiv pare să nu spună nimic util: soluția este fie spre sud, fie spre nord, fie spre este, fie spre vest. Ei și? Este clar că acești algoritmi nu sunt direct implementabili pe un calculator real.
În realitate existența un astfel de algoritm deja înseamnă destul de mult. Înseamnă în primul rînd că problema se poate rezolva algoritmic; vă reamintesc că există probleme care nu se pot rezolva deloc.
În al doilea rînd, se poate arăta că fiecare algoritm nedeterminist se poate transforma într-unul determinist într-un mod automat. Deci de îndată ce știm să rezolvăm o problemă într-un mod nedeterminist, putem să o rezolvăm și determinist! Transformarea este relativ simplă: încercăm să mergem pe toate drumurile posibile în paralel, pe fiecare cîte un pas. (O astfel de tehnică aplicată în cazul labirintului se transformă în ceea ce se cheamă ``flood fill'': evoluez radial de la poziția de plecare în toate direcțiile).
Clasa tuturor problemelor care se pot rezolva cu algoritmi nedeterminiști într-un timp polinomial se notează cu NP (Nedeterminist Polinomial). Este clar că orice problemă care se află în P se află și în NP, pentru că algoritmii determiniști sunt doar un caz extrem al celor determiniști: în fiecare moment au o singură alegere posibilă.
Din păcate transformarea într-un algoritm determinist se face
pierzînd din eficiență. În general un algoritm care operează în
timp nedeterminist polinomial (NP) poate fi transformat cu ușurință
într-un algoritm care merge în timp exponențial (EXP). Avem deci o
incluziune de mulțimi între problemele de decizie: P ![]() NP
NP
![]() EXP.
EXP.
Partea cea mai interesantă este următoarea: știm cu certitudine că
P ![]() EXP. Însă nu avem nici o idee despre relația de
egalitate între NP și P sau între NP și EXP. Nu există nici
o demonstrație care să infirme că problemele din NP au algoritmi
eficienți, determinist polinomiali! Problema P=NP este cea mai
importantă problemă din teoria calculatoarelor, pentru că de
soluționarea ei se leagă o grămadă de consecințe importante.
EXP. Însă nu avem nici o idee despre relația de
egalitate între NP și P sau între NP și EXP. Nu există nici
o demonstrație care să infirme că problemele din NP au algoritmi
eficienți, determinist polinomiali! Problema P=NP este cea mai
importantă problemă din teoria calculatoarelor, pentru că de
soluționarea ei se leagă o grămadă de consecințe importante.
Problema aceasta este extrem de importantă pentru întreaga matematică, pentru că însăși demonstrarea teoremelor este un proces care încearcă să verifice algoritmic o formulă logică (cum am văzut mai sus de pildă); teoremele la care există demonstrații ``scurte'' pot fi asimilate cu problemele din mulțimea NP (la fiecare pas dintr-o demonstrație putem aplica mai multe metode de inferență, în mod nedeterminist; un algoritm trebuie să ghicească înșiruirea de metode aplicate pentru demonstrarea enunțului); dacă orice problemă din NP este și în P, atunci putem automatiza o mare parte din demonstrarea de teoreme în mod eficient!
Problema P=NP este foarte importantă pentru criptografie: decriptarea este o problemă din NP (cel care știe cheia știe un algoritm determinist polinomial de decriptare, dar cel care nu o știe are în fața o problemă pe care nedeterminist o poate rezolva în timp polinomial). Dacă s-ar demonstra că P=NP acest lucru ar avea consecințe extrem de importante, iar CIA si KGB ar fi într-o situație destul de proastă, pentru că toate schemele lor de criptare ar putea fi sparte în timp polinomial (asta nu înseamnă neapărat foarte repede, dar oricum, mult mai repede decît timp exponențial)!
Mai mult, în 1971 Cook a demonstrat că există o problemă specială
în NP (adică pentru care se poate da un algoritm eficient
nedeterminist), numită problema satisfiabilității (notată cu
SAT). Problema este foarte simplă: dacă se dă o formulă booleană
care cuprinde mai multe variabile, poate fi formula făcută
adevărată dînd anumite valori variabilelor? De pildă formula
![]() devine adevărată
pentru x1=adevărat și x2 arbitrar. SAT este
foarte importantă, pentru că Cook a demonstrat că dacă SAT poate fi
rezolvată în P (adică folosind un algoritm determinist polinomial),
atunci orice problemă din NP poate fi rezolvată în timp
polinomial! Problema satisfiabilității este cumva ``cea mai grea
problemă'' din NP, pentru că rezolvarea oricărei alte probleme din NP
se poate face ``mai repede'' decît a ei. Din cauza asta SAT se
numește o problemă NP-completă.
devine adevărată
pentru x1=adevărat și x2 arbitrar. SAT este
foarte importantă, pentru că Cook a demonstrat că dacă SAT poate fi
rezolvată în P (adică folosind un algoritm determinist polinomial),
atunci orice problemă din NP poate fi rezolvată în timp
polinomial! Problema satisfiabilității este cumva ``cea mai grea
problemă'' din NP, pentru că rezolvarea oricărei alte probleme din NP
se poate face ``mai repede'' decît a ei. Din cauza asta SAT se
numește o problemă NP-completă.
De la Cook încoace s-au mai descoperit cîteva sute de probleme NP-complete. Unele probleme care se ivesc foarte adesea în practică s-au dovedit NP-complete! Acesta este un alt motiv pentru care clasa atît de abstractă NP a problemelor cu algoritmi nedeterminiști este atît de importantă: foarte multe probleme practice au algoritmi polinomiali nedeterminiști, dar cei mai buni algoritmi determiniști iau un timp exponențial!
Iată cîteva exemple de probleme NP-complete:
O cantitate enormă de efort și ingeniozitate a fost risipită pentru
a încerca să se demonstreze că P=NP sau opusul acestei afirmații,
dar nici un rezultat concret nu a fost obținut. Credința
cvasi-unanimă este că P![]() NP, dar numai matematica poate oferi
vreo certitudine...
NP, dar numai matematica poate oferi
vreo certitudine...
Din cauză că foarte multe probleme practice sunt în NP, și ca aparent nu putem avea algoritmi determiniști eficace pentru ele, cercetătorii și-au îndreptat atenția asupra unor clase noi de algoritmi, care vor face obiectul secțiunilor următoare.
În secțiunile care urmează folosim tot timpul premiza nedemonstrată că P![]() NP. Dacă P=NP, atunci problemele pe care
ne batem capul să le rezolvăm prin metode ciudate pot fi de fapt
rezolvate exact și eficient, așa că restul articolului cade și nu
se mai ridică.
NP. Dacă P=NP, atunci problemele pe care
ne batem capul să le rezolvăm prin metode ciudate pot fi de fapt
rezolvate exact și eficient, așa că restul articolului cade și nu
se mai ridică.
Foarte multe probleme de optimizare se dovedesc a fi NP-complete3: probleme în care vrem să calculăm maximumul sau minimumul a ceva. Bine, dar dacă de fapt mă mulțumesc să obțin o valoare care nu este chiar optimă, dar este ``suficient de aproape''? Poate în acest caz complexitatea problemei poate fi redusă, și sunt în stare să scriu un algoritm eficient... (polinomial). Avem deci de a face cu un compromis:
solutie optima; solutie sub-optima:
<-------------->
algoritm NP sau algoritm polinomial
algoritm exponential
Într-adevăr, această metodă se bucură de un oarecare succes, dar nu de unul general. Algoritmii care rezolvă o problemă de optimizare în speranța unui rezultat sub-optimal se numesc ``algoritmi aproximativi''.
Există o sumedenie de rezultate în ceea ce privește problemele de
optimizare și aproximările lor. Se demonstrează că unele probleme
pot fi foarte bine aproximate (putem obține soluții cît dorim de
aproape de optim în timp polinomial), altele pot fi aproximate numai
în anumite limite (de exemplu putem obține soluții de 2 ori mai
slabe, dar deloc mai bune), sau altele nu pot fi aproximate deloc (în
ipoteza că P![]() NP).
NP).
Teoria algoritmilor aproximativi este relativ recentă (deși ideea există de multă vreme), iar unele rezultate sunt extrem de complicate. Ne vom mulțumi să dăm niște exemple pentru a ilustra algoritmi aproximativi în acțiune, și tipul de rezultate care se pot obține.
Vom ilustra două rezultate diferite din teoria algoritmilor aproximativi: algoritmi de aproximare relativă, algoritmi de aproximare absolută a soluției (lămurim terminologia imediat).
Să notăm o instanță a unei probleme cu I. Fie OPT(I) valoarea soluției optime pentru acea instanță (care există, dar pe care nu știm s-o calculăm eficient), și fie A(I) valoarea calculată de algoritmul nostru aproximativ. Numim aproximația absolută dacă există un număr K, independent de instanța I, care are proprietatea că |OPT(I) - A(I)| < K. Numim aproximația relativă dacă există un R (numit ``performanță'') astfel ca pentru orice instanță I avem (A(I) / OPT(I)) < R (dacă problema caută un maximum, atunci fracția din definiție trebuie inversată).
Iată o variantă a problemei rucsacului care este NP-completă (nu am discutat deloc în acest articol despre cum se demonstrează așa ceva, așa că trebuie să mă credeți pe cuvînt), dar pentru care se poate obține cu foarte mare ușurință un algoritm aproximativ relativ eficient.
Se dau o mulțime (mare) de rucsaci de capacitate egală (cunoscută, un număr natural). Se mai dă o mulțime finită de obiecte, fiecare de un volum cunoscut (număr natural). Întrebarea este: care este numărul minim de rucsaci necesari pentru a împacheta toate obiectele?
Problema rucsacului are un algoritm de aproximare relativă cu performanță 2.
Algoritmul este banal: metoda ``greedy'': pune de la stînga fiecare greutate în primul rucsac liber:
Date de intrare: nrobiecte, capacitate, marime[1..nrobiecte]
Initializari:
o, folositi := 1, 0
do o <= nrobiecte -> liber[o] := capacitate od
Algoritm:
o := 1
do o <= nrobiecte ->
r := 1
do (liber[r] < marime[o]) -> r := r+1
od
folositi, liber[r], o :=
max(r, folositi), liber[r] - marime[o], o+1
od
Cum demonstrăm că performanța relativă este 2? Foarte simplu: să observăm că la sfîrșitul algoritmului nu pot exista doi rucsaci folosiți pe mai puțin de jumătate amîndoi, pentru că atunci conținutul celui de-al doilea ar fi fost vărsat în primul. Cu alte cuvinte, la terminare avem: liber[r] < 1/2 capacitate. Dar dacă însumăm pentru toți rucsacii, vom avea că spațiul liber este mai puțin de jumătate din cel disponibil, deci cel ocupat este mai mult de jumătate. Dar dacă obiectele au mărime totală M, atunci orice-am face nu putem folosi mai puțin de M spațiu total pentru a le împacheta. Dar noi am folosit mai puțin de M + M = 2M, deci algoritmul are performanță 2. QED.
Vom folosi o altă problemă NP-completă, pentru care avem imediat un algoritm de aproximare relativă de performanță 2, dar pentru care vom demonstra că nu există nici un algoritm de aproximare absolută.
Problema este cea a acoperirii unui graf, enunțată mai sus. Ca problemă de optimizare, ea se enunță astfel: ``care este numărul minim de vîrfuri care trebuie ``acoperite'' astfel ca toate muchiile dintr-un graf să fie atinse?''
Pentru această problemă algoritmul greedy nu face multe parale ca algoritm de aproximare. Există însă un algoritm relativ simplu, cu performanță 2, care se folosește însă de un alt algoritm clasic, cel al ``cuplării'' (matching). Fără a intra în detalii, există un algoritm polinomial relativ sofisticat pentru a calcula cuplări maximale pe grafuri4. Calculăm o cuplare maximală, după care luăm capetele tuturor muchiilor care o formează: astfel obținem o acoperire (ușor de demonstrat) care e cel mult dublă ca mărime față de optim (pentru că în optim trebuie să se găsească cel puțin cîte un vîrf pentru fiecare muchie din cuplare, iar noi am luat cîte două).
Iată și un rezultat negativ interesant: pentru orice K fixat, nu există nici un algoritm care să dea pentru problema acoperirii o soluție aproximativă absolută la distanța K de cea optimă pentru orice instanță. Demonstrația este foarte simplă, odată ce ai văzut ideea, și se bazează pe ``tehnica amplificării''. Iată cum se face, prin reducere la absurd:
Să presupunem că avem un algoritm A care calculează pentru orice graf o acoperire care este cu cel mult K noduri mai mare ca cea optimă (K e fixat). Cu alte cuvinte |OPT(G) - A(G)| < K. Să luăm o instanță arbitrară a problemei cuplării, G. Formăm un nou graf G1 din G, care nu este conex, și care constă din K+1 copii ale lui G, alăturate. Aceasta este o instanță perfect corectă a problemei acoperirii, așa că rulăm pe ea algoritmul nostru A. Acesta va oferi o acoperire care are cel mult cu K noduri mai mult decît acoperirea optimă. (Vă reamintesc notațiile: OPT(G) este valoarea optimă: numărul minim de noduri pentru a acoperi muchiile, iar A(G) este valoarea calculată de algoritmul nostru.
Datorită faptului că cele K+1 copii ale lui G sunt neconectate, optimumul pentru G1 este reuniunea a K+1 optimumuri pentru G. Din cauza asta avem relația OPT(G1) = (K+1) OPT(G). Fie acum H copia lui G pe care A a marcat cele mai multe vîrfuri; atunci A(G1) <= (K+1) A(H). Dar din proprietățile lui A avem: |OPT(G1) - A(G1)| < K, sau |(K+1) OPT(H) - (K+1) A(H)| < K, ori |OPT(H) - A(H)| < K/(K+1) < 1. Însă știm că OPT(H) și A(H) sunt numere naturale, deci am obținut OPT(H) = A(H)!
Asta înseamnă că dacă avem un algoritm aproximativ absolut pentru problema acoperirii, putem imediat construi un algoritm exact la fel de rapid. Ori asta ar însemna că P=NP, ceea ce am presupus fals.
Exemplele pe care le-am ales sunt în mod deliberat simple; teoria algoritmilor aproximativi este în plină dezvoltare și are rezultate foarte spectaculoase și în general complicate. În orice caz, aplicabilitatea ei este imediată, pentru că multe probleme practice care nu pot aștepta au numai rezolvări aproximative.
O tehnică foarte spectaculoasă pentru rezolvarea problemelor este cea a folosiri numerelor aleatoare. Practic algoritmii aleatori sunt identici cu cei obișnuiți, dar folosesc în plus o nouă instrucțiune, care s-ar putea chema ``dă cu banul''. Această instrucțiune generează un bit arbitrar ca valoare.
În mod paradoxal, incertitudinea ne poate oferi mai multă putere...
La ce se folosește aleatorismul? Să ne amintim că în general complexitatea unei probleme este definită luînd în considerare cea mai defavorabilă instanță. De exemplu, pentru problema comis voiajorului, faptul că această problemă este NP-completă nu înseamnă că nu putem rezolva nici o instanță a ei, ci că există instanțe pentru care algoritmii cunoscuți nu au prea multe șanse să termine în curînd.
Acest lucru este adevărat și pentru alte clase de algoritmi; de pildă algoritmul quicksort are pentru majoritatea vectorilor de intrare o comportare O(n log n). Dacă însă datele de intrare sunt prost distribuite, atunci quicksort poate face n2 comparații. Pentru n=100 asta înseamnă de 10 ori mai mult! Numărul de instanțe pentru care quicksort este slab este mult mai mic decît numărul de instanțe pentru care merge bine. Ce te faci însă dacă într-un anumit context lui quicksort i se dau numai date rele? (Datele preluate din măsurători reale sunt foarte rar complet uniform distribuite). O soluție paradoxală constă în a amesteca aleator vectorul înainte de a-l sorta.
Complexitatea medie (average case) a lui quicksort este O(n log n). Complexitatea în cazul cel mai rău (worst case) este O(n2). Dacă datele vin distribuite cu probabilitate mare în zona ``rea'', atunci amestecîndu-le putem transforma instanțe care pică în zona ``worst-case'' în instanțe de tip ``average-case''. Firește, asta nu înseamnă ca nu putem avea ghinion, și ca amestecarea să producă tot o instanță ``rea'', dar probabilitatea ca acest lucru să se întîmple este foarte mică, pentru că quicksort are puține instanțe rele5.
Acesta este un caz de folosire a aleatorului pentru a îmbunătăți performanța medie a unui algoritm.
Cîteodată cîștigul este și mai mare, pentru că putem rezolva probleme NP-complete foarte rapid folosind aleatorismul. De obicei avem însă un preț de plătit. Cînd folosim algoritmi din clasa prezentată mai jos, putem risca să nu primim răspunsul corect.
Evoluția unui algoritm care folosește numere aleatoare nu mai depinde numai de datele de intrare, ci și de numerele aleatoare pe care le generează. Dacă are ``noroc'' algoritmul poate termina repede și bine; dacă dă prost cu zarul, ar putea eventual chiar trage o concluzie greșită. (În cazul quicksort de mai sus răspunsul este întotdeauna corect, dar cîteodată vine mai greu. Aceasta este diferența dintre algoritmii Monte Carlo, mereu corecți, și cei Las Vegas, care pot uneori, rar, greși.)
Vom defini acum algoritmii probabiliști pentru probleme de decizie (țineți minte, la care răspunsul este Da sau Nu). Majoritatea problemelor pot fi exprimate în forma unor probleme de decizie, deci simplificarea nu este prea drastică.
Există două clase de algoritmi probabiliști, dar ne vom concentra atenția numai asupra uneia dintre ele, pentru care vom da și două exemple simple și spectaculoase. Vom defini totodată clasa problemelor care pot fi rezolvate probabilist în timp polinomial, numită RP (Random Polinomial).
Observați că dacă indicăm de la început care sunt numerele aleatoare care vor fi generate, evoluția algoritmului este perfect precizată.
Definiție: O problemă de decizie este în RP dacă există un algoritm aleator A care rulează într-un timp polinomial în lungimea instanței (nc pentru un c oarecare), și care are următoarele proprietăți:
De cine este dată ``probabilitatea'' de mai sus? De numărul de șiruri aleatoare. Cînd rulăm un algoritm aleator pentru o instanță I avem la dispoziție 2nc șiruri aleatoare de biți; pentru unele dintre ele algoritmul răspunde ``Da'', pentru celelalte răspunde ``Nu''. Ceea ce facem este să numărăm pentru cîte șiruri algoritmul ar răspunde ``da'' și să facem raportul cu 2nc. Aceasta este probabilitatea ca algoritmul să răspundă ``da''. Opusul ei este probabilitatea să răspundă ``nu''.
O tehnică foarte simplă de amplificare poate crește nedefinit această probabilitate: dacă executăm algoritmul de 2 ori pe aceleași date de intrare, probabilitatea de a greși pentru răspunsuri ``nu'' rămîne 0. Pe de altă parte, ajunge ca algoritmul să răspundă măcar odată ``da'' pentru a ști că răspunsul este ``da'' cu siguranță! Din cauza asta, dacă probabilitatea de eroare este p pentru algoritm, executînd de k ori probabilitatea coboară la pk (nu uitați ca p este subunitar, ba chiar sub 1/2). Această metodă se numește ``boost'' în engleză, și face dintr-un algoritm probabilist slab ca discriminare o sculă extrem de puternică!
Pentru a scădea probabilitatea de eroare a unui algoritm care poate greși cu probabilitatea p pînă sub o limită dorită siguranta, se procedează astfel:
raspuns, probabilitate = nu, 1
do (raspuns = nu) and (probabilitate > siguranta) ->
raspuns, probabilitate := executa(algoritm), probabilitate * p
od
Iată un exemplu și o aplicație al algoritmilor aproximativi.
Fie un polinom de mai multe variabile, x1, x2, ... xn. Acest polinom poate fi descris printr-o formulă aritmetică, de pildă: (x1 + 1) (x2 + 1) ... (xn + 1). Întrebarea este: este acest polinom identic nul sau nu?
Desigur, o posibilitate este de a ``expanda'' acest polinom în formă canonică (sumă de produse), și de a compara fiecare coeficient cu 0. Dar în general această operație poate lua un timp exponențial! (De exemplu polinomul anterior generează 2n termeni!).
Soluția este să ne bazăm pe două proprietăți elementare ale polinoamelor:
De aici rezultă că:
Pentru polinomul de mai sus gradul este n, și putem alege pentru K de exemplu Zp, unde p este un număr prim relativ mare în raport cu n (de două ori mai mare ajunge!).
Alegînd arbitrar numerele v1, v2, ..., vn în Zp și evaluînd q(v1, v2, ..., vn) mod p, putem imediat afirma cu probabilitate mare > 1 - n/p despre q dacă este nul sau nu! Observați că evaluarea polinomului nu este prea costisitoare, putîndu-se face în timp polinomial în lungimea expresiei care descrie polinomul.
Folosind metoda de ``boost'' putem crește rapid siguranța noastră despre rezultatul algoritmului.
Iată și o aplicație imediată a acestei proprietăți.
Se dau doi arbori, cu rădăcina precizată. Sunt acești doi arbori ``izomorfi'' (identici prin re-ordonarea fiilor)? Această problemă este surprinzător de dificilă pentru un algoritm determinist (am impresia chiar că este NP-completă). Iată însă o soluție aproape imediată: construim pentru fiecare arbore cîte un polinom care nu depinde de ordinea fiilor unui nod, în așa fel încît dacă și numai dacă arborii sunt izomorfi polinoamele sunt egale. Apoi pur și simplu testăm ca mai sus dacă polinomul diferență este nul.
O metodă de a asocia recursiv un polinom unui arbore este de pildă următoarea: fiecărui nod îi asociem o variabilă xk, unde k este înălțimea nodului (distanța pînă la cea mai depărtată frunză). Frunzele vor avea toate asociate variabila x0. Apoi asociem nodului v de înălțime k cu fii v1, ... vl polinomul fv = (xk - fv1) (xk - fv2) ... (xk - fvl). Se arată ușor că polinoamele sunt egale pentru arbori izomorfi, bazîndu-ne pe unicitatea descompunerii în factori a unui polinom. Gradul polinomului asociat unui nod este egal cu suma gradelor fiilor, care la rîndul ei este egală cu numărul de frunze care se află sub acel nod (cum se demonstrează imediat prin inducție după înălțime). Și asta-i tot!
Pentru a încheia secțiunea, să observăm că singurul algoritm eficient cunoscut pentru a verifica primalitatea unui număr este tot probabilist7! Pentru că numerele prime mari stau la baza criptografiei cu cheie publică în sistemul RSA (probabil cel mai răspîndit la ora actuală), iată că unele dintre cele mai importante aplicații se bazează indirect pe algoritmi probabiliști. Nimeni nu va putea obiecta asupra utilității lor!
Adesea trebuie luate decizii cu informații incomplete. Un caz particular este luarea de decizii pe măsură ce datele devin disponibile. Deciziile afectează viitorul, dar sunt luate fără a avea cunoștințe despre datele viitoare. Sa vedem în acțiune un exemplu foarte simplu:
Se pune problema: ce este mai bine: să închiriezi sau să cumperi schiuri? (Vom presupune că prețul schiurilor este constant de-a lungul timpului, ca să simplificăm problema). Dilema constă din faptul că în fiecare sezon, nu știi dacă te vei mai duce odată. Dacă le cumperi și nu te mai duci, ai dat banii degeaba. Dacă le tot închiriezi și te duci des, s-ar putea să le plătești de mai multe ori. Totuși, trebuie să iei o decizie. Pe care?
Există un răspuns foarte simplu, care promite nu că dă rezultatul cel mai ieftin în orice circumstanță, ci doar că nu vei cheltui de două ori mai mult decît în cazul în care ai face decizia perfectă (decizia perfectă este cea care știe precis dacă te vei mai duce, și de cîte ori; ea nu este accesibilă decît ``post-factum'', deci este pur teoretică).
Algoritmul este: închiriezi schiuri pînă ai dat pe chirie costul schiurilor. După aceea dacă mai vrei să mergi le cumperi. Voi demonstra rapid că în felul ăsta orice s-ar întîmpla nu pierzi mai mult de jumate din banii pe care i-ai fi cheltuit în cazul ideal.
Avem 3 posibilități:
Orice altă schemă folosești pentru a decide cumpărarea, există un scenariu în care poți cheltui mai mult de dublu față de optim.
Algoritmii on-line apar foarte natural într-o mulțime de situații: de exemplu în rețele de calculatoare, algoritmii care decid traseul unui pachet cu informații sunt algoritmi on-line; dacă decid trasee proaste, rețeaua poate deveni supra-aglomerată în viitor; astfel de algoritmi nu au idee despre cererile viitoare, așa că acționează cu informație incompletă.
Un alt exemplu este în sistemele de operare: algoritmii după care cache-urile (sau sistemele de memorie virtuală) aleg paginile care trebuie înlocuite. Alegerea aceasta nu poate fi optimă în absența informațiilor despre viitoarele cereri. Cu toate acestea, anumite alegeri sunt mai bune decît altele.
Un al treilea exemplu, tot din contextul sistemelor de operare, este al algoritmilor de planificare, care trebuie să stabilească în ce moment se execută fiecare proces pe un calculator (paralel). Acolo unde minutul de rulare costă o grămadă de bani, deciziile trebuie să risipească cît mai puțin timp. Însă job-uri pentru prelucrare sosesc dinamic, așa că algoritmii trebuie să facă față unui mediu în continuă schimbare.
Algoritmii on-line sunt în general analizați comparîndu-i cu algoritmii off-line, care ar avea înainte de a face deciziile informații perfecte despre toate cererile viitoare. Este clar că informația aceasta este un mare avantaj, așa că în general algoritmii on-line au performanțe mult mai proaste decît cei corespunzători off-line.
Cercetările în acest domeniu sunt doar la început; se explorează și variante de algoritmi hibrizi on/off-line, în care algoritmul are o idee despre viitor, dar nu neapărat o vedere completă. Asta nu face întotdeauna sarcina algoritmului mai simplă, pentru că adesea problema cu informație completă este NP-completă...
În acest articol am trecut razant printr-o grămadă de probleme fascinante. Iată recapitulate sumar conceptele esențiale întîlnite: