Robustness analysis in JavaBayes

The core inference engine in JavaBayes provides support for robustness analysis of Bayesian networks. Robustness analysis employs sets of distributions to model perturbations in the parameters of a probability distribution [1,2,14]. Robust Bayesian inference is the calculation of bounds on posterior values given such perturbations.

Motivation

In the real world we can rarely meet all the assumptions of a Bayesian model. First, we have to face imperfections in our beliefs, either because we have no time, resources, patience, or confidence to provide exact probability values. Second, we may deal with a group of disagreeing experts, each specifying a particular distribution. Third, we may be interested in abstracting away parts of a model and assessing the effects of this abstraction.

There is some empirical evidence that Bayesian networks are not too sensitive to parameters; this is due to the fact that many classic examples of Bayesian networks are sparse graphs, with probability values that are close to zero or one (for example, noisy functions have probability values that are only zero or one). When that happens, you're lucky because robustness is likely to be present. In other words, if changes in one variable do not affect many variables, and changes are not large relative to the magnitude of the numbers, then it is likely that these changes will not produce significant variations in inferences.

Situations where probability values are not very close to zero-one, or where the graph is heavily inter-connected, are situations where robustness may falter. Another situation is model building, where some parameter are not entirely specified, and the question is how much effort should be spent nailing down their values. A serious analysis of a network must consider the possibility of robustness problems, or at least assess how robust the model is. That's the aspect of inference that JavaBayes is trying to address.

Research on Bayesian networks has not fully explored the robustness analysis aspect of inference, due to the lack of algorithms for inferences with convex sets of distributions. JavaBayes is the first Bayesian network engine that provides facilities that explicitly account for perturbations in probabilistic models.

Algorithms for robust Bayesian analysis

Robust Bayesian inference in multivariate structures such as Bayesian networks is a complex algorithmic problem. Usually, the objective of robustness analysis is to obtain the interval that contains all values of a certain quantity of interest, given all possible perturbations in a probabilistic model. Models that attempt to combine Bayesian networks with probability intervals have faced great difficulties. Even though particular classes of probability intervals are amenable to analysis and some brute-force algorithms are possible, there has been no general model of probability intervals with the same style of efficient propagation used in Bayesian networks.

JavaBayes contains two classes of algorithms for robustness analysis:

• Local algorithms, where the perturbations in a Bayesian network are associated with the individual nodes of the network.
• Global algorithms, where perturbations are associated with the whole joint distribution represented by a Bayesian network.

If you have an application that requires use of robustness analysis, I would be grateful if you could send me email explaining what the application is and how you used the system.

The algorithms in JavaBayes employ some recent results to reduce the complexity of robustness analysis. The starting point is the theory of Quasi-Bayesian behavior, proposed in 1980 by Giron and Rios. This theory builds a complete decision making model based on convex sets of probability measures.

A complete discussion of all these issues and an exposition of algorithms can be found at http://www.cs.cmu.edu/~qbayes/Tutorial/.

Global neighborhoods

Consider first the algorithms for global robustness analysis, which are activated through the Edit Network dialog.

Suppose you set a network to represent a multivariate constant density ratio class. You can do this in the Edit Network dialog. If you save the network with the global neighborhood set (in the BIF 0.15 format), you should see the property:

network Example {
	property credal-set constant-density-ratio 1.2;
}

When an inference is requested, the algorithm for global neighborhoods with density ratio classes will be called. The parameter that defines the class in the example is 1.2. If this parameter is smaller than zero, the parameter is automatically set to one (so that it has no effect); if it is smaller than one, then its inverse is used (the parameter has to be larger than one).

Take another example. Suppose a network is declared with the credal-set epsilon-contaminated property:

network Example {
	property credal-set epsilon-contaminated 0.1;
}

then the algorithm for global neighborhoods with $\epsilon$-contaminated classes will be called, using 0.1 as the definition parameter for the $\epsilon$-contaminated class. If this parameter is smaller than zero or larger than one, inferences assume the parameter to be zero.

There are four possible global neighborhoods for a network:

network Example {
	property credal-set constant-density-ratio 1.1;
}

network Example {
	property credal-set epsilon-contaminated 0.1;
}

network Example {
	property credal-set constant-density-bounded 1.1;
}

network Example {
	property credal-set total-variation 0.1;
}

The parameter for the constant density bounded class behaves as the parameter for the constant density ratio class; the parameter for the total variation class behaves as the parameter for the $\epsilon$-contaminated class.

If any of the credal-set properties above are present, the result is a pair of functions, the lower and the upper bounds for the posterior marginals.

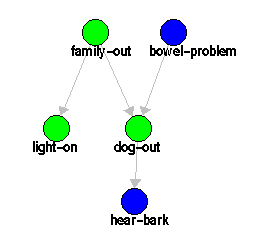
Consider the example discussed in Section , taken from [4].

The problem represents several facts about a family with a dog; the dog barks under some circumstances, and the lights are on under some circumstances. Running this problem in JavaBayes as a standard Bayesian problem , you get:

Posterior distribution:
probability (  "light-on" ) { //1 variable(s) and 2 values
	table 0.23651916875671802 0.763480831243282 ;
}

Now try to perform a robustness analysis by adding say an epsilon-contamination of 0.1. This roughly means that you expect the Bayesian network description to be correct 90 percent of the time, but in 10 percent of the cases you would expect any other joint distribution to be possible. Notice this is a somewhat radical model of uncertainty as you are allowing for 0.1 in probability mass to be concentrated in arbitrary sets or events. Add the following line in the network block:

	property credal-set epsilon-contaminated 0.1;

and load the new network description into JavaBayes: You will get the result:

Posterior distribution:
 envelope (  "light-on" ) { //1 variable(s) and 2 values
	table lower-envelope 0.21286725188104622 0.6871327481189539 ;
	table upper-envelope 0.31286725188104625 0.7871327481189538 ;
}

These functions are the lower and upper bounds respectively.

Local neighborhoods

Local perturbations to a network can be inserted as sets of conditional densities associated with variables in the network. Each variable can be associated to a polytope in the space of densities.

To associate a variable with a set of densities, you have to insert the vertices of the set of densities. Go to the Edit variable window and mark some variable as a Credal set with extreme points. Insert the number of vertices of the set of distributions. Then edit these densities in the Edit function window.

You can also insert the vertices of a set of densities directly into the describing a network; JavaBayes simply asks you to determine which vertice you are referring to. In the example above, suppose you want to define an interval for the probability of family-out. You can write a file in the BIF0.15 format with the following declaration:

probability ( "family-out" ) { //1 variable(s) and 2 values
	table 0.15 0.85 ;
	table 0.25 0.75 ;
}

This defines an interval $0.15 \leq p(family-out) \leq 0.25$. You can also insert more vertices if that's appropriate, but note that for a binary variable that does not add any information.

If you insert the set of densities above, then you get:

Posterior distribution:
 envelope (  "light-on"  "<Transparent:family-out>" ) { //2 variable(s) and 2 values
	table lower-envelope 0.23651916875671802 0.6792901716068643 ;
	table upper-envelope 0.3207098283931358 0.763480831243282 ;
}

This indicates the lower and upper bounds for the probability of light-on given the evidence, and also indicates which sets of densities affect the result (in this case, the densities for family-out).