DiTops' propagator is intended to maintain the consistency of a set of values that are distributed over the nodes in a graph. In particular it maintains the time bounds of the operations (the nodes) that DiTops is attempting to schedule so that the time bounds are consistent with the constraints (edges) between the operations. Each operation represents an activity with a start time and a finish time. The user can define both absolute and relative constraints for these start and finish times. These constraints limit the the start and finish time values. These limits are described by maintaing an upper and lower bound for each of the time values. The purpose of the propagator is to determine a consistent set of values for the bounds given the set of constraints.
The propagator attempts to create the "loosest" set of bounds for an activities start and finish times. The "loosest" set of bounds allows the scheduling system the most leeway in assigning resources to the activity. In achieving the "loosest" set, the propagator doesn't violate any of the constraints.
The propagator has to deal with a varying number of constraints, in an efficient manner. The number of constraints can increase via user action or whenever a scheduling decision is made. The number of constraints can decrease via a user action, or whenever a scheduling decision retracts a previous scheduling decision. Whenever a scheduling decision changes the number of constraints, the propagator is invoked to ensure that the bounds on the unscheduled values are consistent with the decision.
When allowed by the user, a scheduling decision can violate constraints. This violation presents the propagator with several choices when propagating the results of the decision. The overall rule is, if the propagator can create a set of values consistent with the constraints it should do so. If it can't create such a set, then it asks the scheduling system to fix its decisions so such a consistent set can be found. In addition, the set of bounds should be the "loosest" set possible.

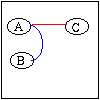
The set of constraints on a bound can be ordered by how much each constraint is affecting the bound. This ordering allows the propagator to quickly determine the source of the current bound value. An example of a set of constraints is given in the diagram to the right. In this diagram Operation A is constrained to have the same-end as Operation B (indicated by blue line) and A is also constrained to occur before C (indicated by the red line). Given that B has a finish time of 5, and C has a latest start time at 5, an ordering of how these constraints affect A's finish time is given below.
Earliest Latest
bound bound
2 3 5 7 8
---------------|-----| |----------|--------|-------
EAD Same-End-A Before-C Same-End-A DD
Also note that the A's finish time has two absolute constraints the Earliest Arrival Date (EAD) and the Due Date (DD).
To always ensure that constraints aren't violated, the propagator follows these two rules:
These rules are similar to the way the AR-4 arc-consistency propagator determines the reason values have been deemed inconsistent. By following these rules in an arc-consistenc manner, the propagation is both efficient and produces an arc-consistent graph. An arc-consistent graph though produces schedules with slack time between the operations. To remove as much of the slack time as possible, a path-consistent algorithm is currently used.
Maintaining the ordered set of constraints is both expensive in space and time. The ordered set consumes O(n^2) space where n is the number of nodes, since every node could be connected to every other node. Since the set is ordered, changes to a set member means the set needs to be ordered again. While many possible algorithms for efficiently maintaining the list as ordered (binary tree, insertion sort) are possible, we note that only the relaxation rule uses the elements of the list and then only the first 2 elements of the ordered list. This observation leads us to the implementation of only maintaining the first two elements of the list as a cache, and re-calculating the list if more elements are needed.
We need to re-calculate the list when rule #2 applies, and the most restrictive constraint is no longer the most restrictive constraint. We don't need to re-calculate the entire list when rule #1 applies, because we can just insert the more restrictive constraint in the first element of the cache, and move the previously most restrictive element to the second position. We also have to do extra work to maintain the correctness of the second position when rule #1 doesn't apply (because the changed constraint isn't the most restrictive) but the changed constraint is more restrictive than the second list member.
This maintenance of just the tip of the list, is similar to what the arc-consistency algorithm AR-6 does. However, we have to do more work because of the dynamic nature of our constraints. It is an empirical question whether maintaing the entire list is more compute time efficient or whether keeping the tip and recalculating is more efficient. The keeping of only the list tip was a win for the AR-6 algorithm, and the space efficiency is important also. However, some effort should go into quantifying what is saved.
This experiment is aimed at showing the requirement for relaxation. I have abstracted from the securing airport problem 2 small tasks each with a synchronization activity (like securing the airport). Scheduling these problems with tight bounds is difficult.


