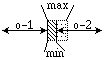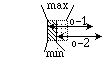Temporal Constraints in DiTops

In DiTops we have operations that represent activities. These operations have sets of values that define temporal events of interest. An operation can also have constraints that define the acceptable values for the temporal events. A constraint defines a relationship between the values in one operation and either an absolute value, or the values in a different operation. The propagator traverses the graph of operations and constraints and either creates for each operation a set of acceptable values consistent with the constraints, or detects that for some operations no values are consistent with the constraints. This page describes the set of constraints that apply to the start and completion time bounds for the activity represented by an operation. The propagator uses these constraints to create an arc-consistent set of values for the start/completion times.

The constraints on the start and completion times can be broken into two sets. The first set represents relationships of the constrained time to some user specified absolute time. I call these Absolute Constraints. The second set of constraints represent a binary relationship between two operations. I call these Relative Constraints.

All of these constraints are defined as constraints on a particular time-bound of an operation.

Absolute Constraints

The set of Absolute Constraints currently in use are given in the following table:

The obvious hole in the set of Absolute constraints is a Latest Start constraint. That constraint does not currently exist mainly because no application has required it. DiTops can relax these absolute constraints to find a feasible solution to some scheduling problem. Currently DiTops allows the Due Date and EAD to be relaxed. These are the correct constraints to relax for some domains. However, if one is attempting to fire a rocket and only have a short window in which firing is possible, then holding the Due Date as unmovable and relaxing the Earliest Start Time is correct. The "Maximum Deviation" parameter in the above table is intended to allow a partial relaxation of a constraint. The intent is to allow users the ability to specify that these constraints can be relaxed a little if necessary. Allowing a constraint to be Completely relaxed is controlled by other means.

Relative Constraints

The set of Relative Constraints is given in the following table:

Relative Constraints

RELATIONSHIP NAME	Parameters	Semantics
Before	Minimum Offset Maximum Offset	Operation 1 must end before Operation 2 starts. "Sue must get to the airport before boarding the plane."
Starts-before	Minimum Offset Maximum Offset	Operation 1 must start before Operation 2 starts. "While Sue mows the grass, I'll rake the clippings."
Ends-before	Minimum Offset Maximum Offset	Operation 1 must end before Operation 2 ends. "The airport must be cleared before the plane's flight can end."
Same-start	Window Size	Operation 1 and Operation 2 must start within window time of each other. Order of starting is unimportant. "The two nuts, on each side of the rod, should be tightened from both sides to keep the rod from over-turning."
Same-end	Window Size	Operation 1 and Operation 2 must end within a defined time of each other. Order of completion is unimportant. "Loading the fuel, and loading the cargo should be done about the same time."

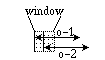
An obvious lack is a windowed relation from the end time of OP-1 to the start time of OP-2 (a windowed "Before"). The semantics of this relation would be that OP-1 should end about the time OP-2 starts. As with the other "windowed" relationships, OP-2 could start before OP-1. OP-2 just can't start too soon before OP-1.

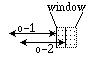
In the Relative Constraints table, the pictures on the right show how a constraint relates the two activities (OP-1 and OP-2). For both activities the start time is represented by the left arrow, and the end time the right arrow. Within the small square the area with slashes () represents the minimum time interval which is the minimum amount the arrows should be separated. The arrows can not be inside the minimum separation area without violating the constraint. In the diagrams with a minimum constraint, the two activities are shown as being as closely aligned as possible. However, the two activities could be separated by more time, up to the maximum separation value, and still not be violating the constraint.

Relation to Allen's Relations

Allen has described a set of relations between time intervals that can be implemented via the relations above. The mapping between Allen's relations and the set of DiTops relations is given in the table below.

The main difference between Allen's interval relations and DiTops's interval relations, is the ability in DiTops to specify an approximate relationship between two intervals. In Allen's interval relations, specific points in time (perhaps with unknown values) are related. DiTop's relations include a range of values either from min to max or within a window and these ranges allow for some uncertainty to be represented. In creating his temporal relations, Allen was setting up an interval temporal logic system, where he could classify all relationships between intervals uniquely. In Allen's temporal logic, he can describe exactly how a specific action will change the world over a period of time. To describe how the world changes over a period of time, Allen invokes the standard closed-world assumption. In contrast, DiTops relationships are intended to model real world activities where all the changes to the world are not fore known and the resultant uncertainties abound.

The desired functionality is different too. Allen wants to model cause-effect where both cause and effect occur over some temporal interval. In this mode, it is computationally cheaper to model relations as between time points. In contrast, DiTops wants to optimize resource utilization or due date satisfaction when scheduling multiple plans. For DiTops, it is computationally cheaper to model relations with some slack. The existence of some slack can help limit the propagation of small changes.